题目内容
在光滑倾斜长轨道上的A点有一个质量为m的物体，已知倾斜轨道与水平方向的倾角为θ．某时刻对物体施加一平行倾斜轨道向上的恒力F，使其由静止开始运动，经过时间t，物体刚好运动到了倾斜轨道上的B点，此时立即将恒力F反向．当经过同样长的时间t，物体刚好回到了倾斜轨道上的A点．由此可以推知（ ）
分析：抓住两段时间内位移大小相等，时间相等，结合运动学公式求出两段过程中的加速度之比，结合牛顿第二定律求出恒力的大小．
解答：解：向上做匀加速直线运动的位移x1=
a1t2，速度v=a1t
恒力F反向后，在时间t内的位移x2=vt-
a2t2．
因为x1=-x2
联立解得
=
．
根据牛顿第二定律得，a1=
，a2=
解得F=2mgsinθ．故B正确，A、C、D错误．
故选B．
| 1 |
| 2 |
恒力F反向后，在时间t内的位移x2=vt-
| 1 |
| 2 |
因为x1=-x2
联立解得
| a1 |
| a2 |
| 1 |
| 3 |
根据牛顿第二定律得，a1=
| F-mgsinθ |
| m |
| F+mgsinθ |
| m |
解得F=2mgsinθ．故B正确，A、C、D错误．
故选B．
点评：本题考查了牛顿第二定律和运动学公式的综合运用，知道加速度是联系力学和运动学的桥梁．
练习册系列答案
相关题目
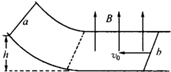如图所示，水平放置的、足够长的光滑金属轨道与光滑倾斜轨道以小圆弧平滑对接．在倾斜轨道上高h=l.8m处放置一金属杆a，在平直轨道靠右端处放置另一金属杆b，平直轨道区域有竖直向上的匀强磁扬．现由静止释放杆a，杆a下滑到水平轨道后即进入磁场，此时杆b的速度大小为v0=3m/s，方向向左．已知ma=2kg，mb=lkg，金属杆与轨道接触良好，g取10m/s2．求：
如右图所示，位于竖直平面内的固定光滑圆环轨道与水平面相切于M点，与竖直墙相切于A点，竖直墙上另一点B与M的连线和水平面的夹角为60°，C是圆环轨道的圆心，D是圆环上与M靠得很近的一点（弧长DM远小于圆环半径）．已知在同一时刻：a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道运动到M点；c球由C点自由下落到M点；d球从D点静止出发沿圆环运动到M点．则（ ）| A、a球比b球先到达M点 | B、b球最先到达M点 | C、c球最先到达M点 | D、a球与d球同时到达M点 |