题目内容
4.己知地球和月球的质量分别为M和m,半径分别为R和r.则在地球表面和月球表面的重力加速度之比为$\frac{M{r}_{\;}^{2}}{m{R}_{\;}^{2}}$,地球和月球的第一宇宙速度之比为$\sqrt{\frac{Mr}{mR}}$.分析 根据万有引力等于重力表示出g,再求出比值;第一宇宙速度是近地卫星的环绕速度,也是最大的圆周运动的环绕速度.
解答 解:根据万有引力等于重力,有$mg=G\frac{Mm}{{R}_{\;}^{2}}$
解得$g=\frac{GM}{{R}_{\;}^{2}}$
$\frac{{g}_{地}^{\;}}{{g}_{月}^{\;}}=\frac{G\frac{M}{{R}_{\;}^{2}}}{G\frac{m}{{r}_{\;}^{2}}}=\frac{M{r}_{\;}^{2}}{m{R}_{\;}^{2}}$
第一宇宙速度是近地卫星的环绕速度,根据$G\frac{Mm}{{R}_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{R}$,即$v=\sqrt{\frac{GM}{R}}$
$\frac{{v}_{地}^{\;}}{{v}_{月}^{\;}}=\frac{\sqrt{\frac{GM}{R}}}{\sqrt{\frac{Gm}{r}}}$=$\sqrt{\frac{Mr}{mR}}$
故答案为:$\frac{M{r}_{\;}^{2}}{m{R}_{\;}^{2}}$,$\sqrt{\frac{Mr}{mR}}$
点评 解决本题的关键是知道第一宇宙速度是近地卫星的环绕速度,在任意一个星球表面物体重力等于万有引力即可求解星球表面的重力加速度.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
14. 如图所示的装置中,已知小轮A的半径是大轮B的半径的$\frac{1}{3}$,A、B在边缘接触,形成摩擦传动,接触点无打滑现象.B为主动轮,B转动时边缘的线速度为v,角速度为ω,则( )
如图所示的装置中,已知小轮A的半径是大轮B的半径的$\frac{1}{3}$,A、B在边缘接触,形成摩擦传动,接触点无打滑现象.B为主动轮,B转动时边缘的线速度为v,角速度为ω,则( )
 如图所示的装置中,已知小轮A的半径是大轮B的半径的$\frac{1}{3}$,A、B在边缘接触,形成摩擦传动,接触点无打滑现象.B为主动轮,B转动时边缘的线速度为v,角速度为ω,则( )
如图所示的装置中,已知小轮A的半径是大轮B的半径的$\frac{1}{3}$,A、B在边缘接触,形成摩擦传动,接触点无打滑现象.B为主动轮,B转动时边缘的线速度为v,角速度为ω,则( )| A. | A轮边缘的线速度为$\frac{1}{3}$v | B. | 两轮边缘的线速度之比vA:vB=1:1 | ||
| C. | A轮的角速度为$\frac{1}{3}$ω | D. | 两轮转动的周期之比TA:TB=3:1 |
12. 在半球形光滑碗内,斜放一根筷子,如图所示,筷子与碗的接触点分别为A、B,则碗对筷子A、B两点处的作用力方向分别为( )
在半球形光滑碗内,斜放一根筷子,如图所示,筷子与碗的接触点分别为A、B,则碗对筷子A、B两点处的作用力方向分别为( )
 在半球形光滑碗内,斜放一根筷子,如图所示,筷子与碗的接触点分别为A、B,则碗对筷子A、B两点处的作用力方向分别为( )
在半球形光滑碗内,斜放一根筷子,如图所示,筷子与碗的接触点分别为A、B,则碗对筷子A、B两点处的作用力方向分别为( )| A. | A点处指向球心O,B点处竖直向上 | |
| B. | 均竖直向上 | |
| C. | A点处指向球心O,B点处垂直于筷子斜向上 | |
| D. | 均指向球心O |
9.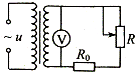 如图所示,理想变压器原、副线圈的匝数比为11:2,原线圈两端的输入正弦交流电压B表达式u=220$\sqrt{2}$sin100πt(V),副线圈两端所接的电压表为理想电压表,定值电阻R0=10Ω,滑动变阻器R的阻值变化范围为0~20Ω,下列说法正确的是( )
如图所示,理想变压器原、副线圈的匝数比为11:2,原线圈两端的输入正弦交流电压B表达式u=220$\sqrt{2}$sin100πt(V),副线圈两端所接的电压表为理想电压表,定值电阻R0=10Ω,滑动变阻器R的阻值变化范围为0~20Ω,下列说法正确的是( )
 如图所示,理想变压器原、副线圈的匝数比为11:2,原线圈两端的输入正弦交流电压B表达式u=220$\sqrt{2}$sin100πt(V),副线圈两端所接的电压表为理想电压表,定值电阻R0=10Ω,滑动变阻器R的阻值变化范围为0~20Ω,下列说法正确的是( )
如图所示,理想变压器原、副线圈的匝数比为11:2,原线圈两端的输入正弦交流电压B表达式u=220$\sqrt{2}$sin100πt(V),副线圈两端所接的电压表为理想电压表,定值电阻R0=10Ω,滑动变阻器R的阻值变化范围为0~20Ω,下列说法正确的是( )| A. | 电压表的示数为40V | |
| B. | 副线圈输出电压的频率为50Hz | |
| C. | 滑动变阻器R消耗功率的最大值为20W | |
| D. | 滑动变阻器滑片向下移动,变压器的输出功率不变 |
16.在远距离输电时,输送的电功率为P,输电电压为U,所用导线电阻率为ρ,横截面积为S,输电导线的长度之和为L,若导线上消耗的电功率为P1,用户得到的电功率为P2,则下列关系式中正确的是( )
| A. | P1=$\frac{{U}^{2}S}{pL}$ | B. | P1=$\frac{pL{P}^{2}}{{U}^{2}S}$ | C. | P2=P-$\frac{{U}^{2}S}{pL}$ | D. | P2=P(1-$\frac{pL{P}^{2}}{{U}^{2}S}$) |

 如图所示,导轨间距L=0.5m,α=37°,B=0.4T,棒的质量为m=0.1kg,金属棒的电阻为R=0.2Ω,其余电阻不计,金属棒与导轨的动摩擦因数μ=0.5,导体棒由静止开始运动,到刚好匀速时,通过导体横截面的电量Q=2C.求:
如图所示,导轨间距L=0.5m,α=37°,B=0.4T,棒的质量为m=0.1kg,金属棒的电阻为R=0.2Ω,其余电阻不计,金属棒与导轨的动摩擦因数μ=0.5,导体棒由静止开始运动,到刚好匀速时,通过导体横截面的电量Q=2C.求: