题目内容
10. 如图所示,导轨间距L=0.5m,α=37°,B=0.4T,棒的质量为m=0.1kg,金属棒的电阻为R=0.2Ω,其余电阻不计,金属棒与导轨的动摩擦因数μ=0.5,导体棒由静止开始运动,到刚好匀速时,通过导体横截面的电量Q=2C.求:
如图所示,导轨间距L=0.5m,α=37°,B=0.4T,棒的质量为m=0.1kg,金属棒的电阻为R=0.2Ω,其余电阻不计,金属棒与导轨的动摩擦因数μ=0.5,导体棒由静止开始运动,到刚好匀速时,通过导体横截面的电量Q=2C.求:(1)棒在运动过程中,任意△t=2s内导体棒在框架上可能扫过的最大面积;
(2)从开始下滑到刚好匀速,导体棒中产生的焦耳热(g=10m/s2).
分析 (1)根据法拉第电磁感应定律和根据闭合电路欧姆定律求解安培力的表达式,根据匀速运动受力平衡求解匀速运动的速度,匀速运动时在△t时间内扫过面积最大,由此求解最大面积;
(2)根据电量计算公式求解金属棒运动的位移,根据能量守恒定律求解产生的焦耳热.
解答 解:(1)金属棒运动时产生的电动势方向从N到M,匀速时,对金属棒受力分析如图所示,
应满足平衡条件:mgsinα=μmgcosα+F安
根据法拉第电磁感应定律应有:E=BLv
根据闭合电路欧姆定律应有:I=$\frac{E}{R}$
又F安=BIL
联立可得:v=1m/s;
由于金属棒匀速时速度最大,所以在△t时间内扫过的最大面积为:Sm=Lv△t=1m2;
(2)根据电量Q=$\overline{I}△t$=$\frac{△Φ}{R}$=$\frac{BLx}{R}$,
可得金属棒运动的位移为:x=2m;
根据能量守恒定律应有:mgxsinα=Q热+$\frac{1}{2}m{v}^{2}$+μmgxcosα
联立可得:Q热=0.35J.
答:(1)棒在运动过程中,任意△t=2s内导体棒在框架上可能扫过的最大面积为1m2;
(2)从开始下滑到刚好匀速,导体棒中产生的焦耳热为0.35J.
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,重点是分析安培力作用下导体棒的平衡问题,根据平衡条件列出方程;另一条是能量,分析涉及电磁感应现象中的能量转化问题,根据动能定理、功能关系等列方程求解.

练习册系列答案
相关题目
3. 如图所示,曲线 I 是一颗绕地球做匀速圆周运动的卫星的轨道示意图,其半径为 R,曲线 II 是一颗绕地球做椭圆运动的卫星的轨道示意图,O点为地球球心,AB为椭圆的长轴,PQ为短轴和椭圆轨道的交点,两轨道和地心都在同一平面内,己知在两轨道上运动的卫星的周期相等,万有引力常量为 G,地球质量为 M,下列说法正确的是( )
如图所示,曲线 I 是一颗绕地球做匀速圆周运动的卫星的轨道示意图,其半径为 R,曲线 II 是一颗绕地球做椭圆运动的卫星的轨道示意图,O点为地球球心,AB为椭圆的长轴,PQ为短轴和椭圆轨道的交点,两轨道和地心都在同一平面内,己知在两轨道上运动的卫星的周期相等,万有引力常量为 G,地球质量为 M,下列说法正确的是( )
 如图所示,曲线 I 是一颗绕地球做匀速圆周运动的卫星的轨道示意图,其半径为 R,曲线 II 是一颗绕地球做椭圆运动的卫星的轨道示意图,O点为地球球心,AB为椭圆的长轴,PQ为短轴和椭圆轨道的交点,两轨道和地心都在同一平面内,己知在两轨道上运动的卫星的周期相等,万有引力常量为 G,地球质量为 M,下列说法正确的是( )
如图所示,曲线 I 是一颗绕地球做匀速圆周运动的卫星的轨道示意图,其半径为 R,曲线 II 是一颗绕地球做椭圆运动的卫星的轨道示意图,O点为地球球心,AB为椭圆的长轴,PQ为短轴和椭圆轨道的交点,两轨道和地心都在同一平面内,己知在两轨道上运动的卫星的周期相等,万有引力常量为 G,地球质量为 M,下列说法正确的是( )| A. | 椭圆轨道的长轴长度为2R | |
| B. | 卫星沿Ⅱ轨道由P点运动到Q点所需要的时间为椭圆轨道运动周期的一半 | |
| C. | 卫星在 I 轨道P点的加速度大小为a1,在II 轨道P 点加速度大小为 a2,则 a1=a2 | |
| D. | 若OA=0.5R,则卫星在 B 点的速率 vB<$\sqrt{\frac{2GM}{3R}}$ |
1. 密立根油滴实验的原理如图所示,两块水平放置的平行金属板与电源相连接,油滴从喷雾器喷出后,通过小孔落到距离为d的两板之间.在强光照射下,观察者可通过显微镜观察油滴的运动.油滴可以视为球形,在经过喷雾器喷嘴时因摩擦而带电.油滴在空气中下落时所受空气阻力大小跟它下落速度v的大小和半径r成正比,即f=krv(k为比例系数).某次实验中先将开关S断开,两极板不带电,一质量为m的油滴落入两板间一段时间后做匀速运动,速度大小为v0.再将开关S闭合,两板间电压为U,油滴在匀强电场中受电场力作用最终向上匀速运动,速度大小仍为v0.油滴受到空气的浮力远小于重力,可以忽略.下列说法正确的是( )
密立根油滴实验的原理如图所示,两块水平放置的平行金属板与电源相连接,油滴从喷雾器喷出后,通过小孔落到距离为d的两板之间.在强光照射下,观察者可通过显微镜观察油滴的运动.油滴可以视为球形,在经过喷雾器喷嘴时因摩擦而带电.油滴在空气中下落时所受空气阻力大小跟它下落速度v的大小和半径r成正比,即f=krv(k为比例系数).某次实验中先将开关S断开,两极板不带电,一质量为m的油滴落入两板间一段时间后做匀速运动,速度大小为v0.再将开关S闭合,两板间电压为U,油滴在匀强电场中受电场力作用最终向上匀速运动,速度大小仍为v0.油滴受到空气的浮力远小于重力,可以忽略.下列说法正确的是( )
 密立根油滴实验的原理如图所示,两块水平放置的平行金属板与电源相连接,油滴从喷雾器喷出后,通过小孔落到距离为d的两板之间.在强光照射下,观察者可通过显微镜观察油滴的运动.油滴可以视为球形,在经过喷雾器喷嘴时因摩擦而带电.油滴在空气中下落时所受空气阻力大小跟它下落速度v的大小和半径r成正比,即f=krv(k为比例系数).某次实验中先将开关S断开,两极板不带电,一质量为m的油滴落入两板间一段时间后做匀速运动,速度大小为v0.再将开关S闭合,两板间电压为U,油滴在匀强电场中受电场力作用最终向上匀速运动,速度大小仍为v0.油滴受到空气的浮力远小于重力,可以忽略.下列说法正确的是( )
密立根油滴实验的原理如图所示,两块水平放置的平行金属板与电源相连接,油滴从喷雾器喷出后,通过小孔落到距离为d的两板之间.在强光照射下,观察者可通过显微镜观察油滴的运动.油滴可以视为球形,在经过喷雾器喷嘴时因摩擦而带电.油滴在空气中下落时所受空气阻力大小跟它下落速度v的大小和半径r成正比,即f=krv(k为比例系数).某次实验中先将开关S断开,两极板不带电,一质量为m的油滴落入两板间一段时间后做匀速运动,速度大小为v0.再将开关S闭合,两板间电压为U,油滴在匀强电场中受电场力作用最终向上匀速运动,速度大小仍为v0.油滴受到空气的浮力远小于重力,可以忽略.下列说法正确的是( )| A. | 油滴带正电 | B. | 油滴的半径为$\frac{mg}{{kv}_{0}}$ | ||
| C. | 油滴所带的电荷量为$\frac{mgd}{U}$ | D. | 电场力对油滴一直做正功 |
2.关于电磁感应现象,下列说法正确的是( )
| A. | 只要闭合回路的磁通量不为零,回路中就有感应电流 | |
| B. | 若感应电流是由原电流变化而产生的,则感应电流的方向总是与原电流的方向相反 | |
| C. | 感应电动势的大小与回路中磁通量的变化率大小成正比 | |
| D. | 当闭合回路的一部分导体在磁场中运动时,速度越大,则感应电流强度也越大 |
20.某兴趣小组在课下用同一灯泡和电容器、电感器及直流电源和有效值等于直流的交流电源,先后完成了如图a、b、c、d所示实验,关于S闭合后现象的说法中正确的是( )


| A. | a、b中小灯泡都不会发光 | |
| B. | a中灯泡不发光,b中小灯泡会发光 | |
| C. | c、d中小灯泡都发光,且明亮程度相同 | |
| D. | c中灯泡发光,d中灯泡发光较暗,甚至看不到发光 |
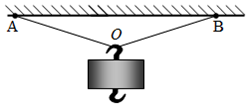 某同学提出了仅运用一个已知质量为m的钩码和一把米尺进行测量的方案.首先,他把钩码直接悬挂在这种棉线上,结果棉线没有断,而且没有发生明显伸长.然后该同学利用如图的装置,得出了该棉线能承受的最大拉力(细线两端点A、B始终位于同一水平线).请你根据该同学已具有的上述器材,回答下列问题(已知重力加速度为g):
某同学提出了仅运用一个已知质量为m的钩码和一把米尺进行测量的方案.首先,他把钩码直接悬挂在这种棉线上,结果棉线没有断,而且没有发生明显伸长.然后该同学利用如图的装置,得出了该棉线能承受的最大拉力(细线两端点A、B始终位于同一水平线).请你根据该同学已具有的上述器材,回答下列问题(已知重力加速度为g): 如图所示,在水平面上有两条长度相同均为2L,间距为L的平行长直轨道,处于竖直向下的匀强磁场中,磁感应强度为B,横置于轨道上长为L的滑杆向右运动,滑杆和轨道电阻很小忽略不计,两者无摩擦且接触良好,轨道两侧分别连接理想电压表理想电流表和外电阻,阻值为R,
如图所示,在水平面上有两条长度相同均为2L,间距为L的平行长直轨道,处于竖直向下的匀强磁场中,磁感应强度为B,横置于轨道上长为L的滑杆向右运动,滑杆和轨道电阻很小忽略不计,两者无摩擦且接触良好,轨道两侧分别连接理想电压表理想电流表和外电阻,阻值为R,