题目内容
一质量为M=0.8kg的中空的、粗细均匀的、足够长的绝缘细管,其内表面粗糙、外表面光滑;有一质量为m=0.2kg、电荷量为q=0.1C的带正电小滑块以水平向右的速度进入管内,如图甲.细管置于光滑的水平地面上,细管的空间能让滑块顺利地滑进去,示意图如图乙.运动过程中滑块的电荷量保持不变.空间中存在垂直纸面向里的水平匀强磁场,磁感强度为B=1.0T.(取水平向右为正方向,g=10m/s2)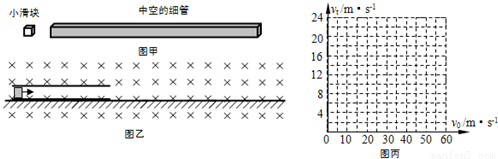
(1)滑块以v=10m/s的初速度进入管内,则系统最终产生的内能为多少?
(2)滑块最终的稳定速度 vt取决于滑块进入细管时的初速度v,请以滑块的初速度v为横坐标、滑块最终稳定时的速度vt为纵坐标,在丙图中画出滑块的vt-v图象(只需画出v的取值范围在0至60m/s的图象).
【答案】分析:(1)滑块进入管中后,滑块做减速运动,管子做加速运动,由动量守恒定律及能量守恒定律可以求系统产生的内能.
(2)求出滑块与管子间没有弹力及摩擦力时的速度,分析滑块以不同速度进入管子时的运动情况,然后作出图象.
解答: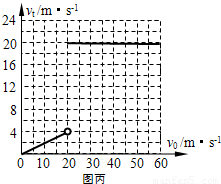 解:(1)小球刚进入管内时受到洛仑兹力为:F洛=qvB=1N,
解:(1)小球刚进入管内时受到洛仑兹力为:F洛=qvB=1N,
由左手定则可知,小球受洛仑兹力方向向上,F洛<mg=2N,
小球与管的下壁有弹力,摩擦使球减速至最终与细管速度相同时,
两者以共同速度v运动,由动量守恒定律:mv=(m+M)v,
解得:v=2 m/s,由能量守恒定律得:
系统产生内能: ,解得:Q=8 J;
,解得:Q=8 J;
(2)当滑块对管的上下壁均无压力时,滑块进入细管的速度满足: ,得:v'=20m/s,
,得:v'=20m/s,
①当小球初速小于v1=20m/s时,F洛<mg,小球与管的下壁有弹力,摩擦力使小球最终与管共速,
系统动量守恒:mv=(m+M)v,代入数据得:vt=0.2v(0<v<20m/s),
②当初速度大于vm时细管离开地面:(M+m)g=qvmB,代入数据得:vm=100m/s,
③当小球初速20m/s≤v≤100m/s时,小球与管的上壁有弹力,摩擦使球减速最终速度为v',即:vt=20m/s;
vt-v图象如图所示.
答:(1)滑块以v=10m/s的初速度进入管内,系统最终产生的内能为8J;
(2)vt-v图象如图所示.
点评:熟练应用左手定则及洛伦兹力公式对小滑块进行受力分析,根据滑块的受力情况分析滑块的运动情况,对各种可能出现的情况是正确解题的关键;本题难度较大.
(2)求出滑块与管子间没有弹力及摩擦力时的速度,分析滑块以不同速度进入管子时的运动情况,然后作出图象.
解答:
 解:(1)小球刚进入管内时受到洛仑兹力为:F洛=qvB=1N,
解:(1)小球刚进入管内时受到洛仑兹力为:F洛=qvB=1N,由左手定则可知,小球受洛仑兹力方向向上,F洛<mg=2N,
小球与管的下壁有弹力,摩擦使球减速至最终与细管速度相同时,
两者以共同速度v运动,由动量守恒定律:mv=(m+M)v,
解得:v=2 m/s,由能量守恒定律得:
系统产生内能:
 ,解得:Q=8 J;
,解得:Q=8 J;(2)当滑块对管的上下壁均无压力时,滑块进入细管的速度满足:
 ,得:v'=20m/s,
,得:v'=20m/s,①当小球初速小于v1=20m/s时,F洛<mg,小球与管的下壁有弹力,摩擦力使小球最终与管共速,
系统动量守恒:mv=(m+M)v,代入数据得:vt=0.2v(0<v<20m/s),
②当初速度大于vm时细管离开地面:(M+m)g=qvmB,代入数据得:vm=100m/s,
③当小球初速20m/s≤v≤100m/s时,小球与管的上壁有弹力,摩擦使球减速最终速度为v',即:vt=20m/s;
vt-v图象如图所示.
答:(1)滑块以v=10m/s的初速度进入管内,系统最终产生的内能为8J;
(2)vt-v图象如图所示.
点评:熟练应用左手定则及洛伦兹力公式对小滑块进行受力分析,根据滑块的受力情况分析滑块的运动情况,对各种可能出现的情况是正确解题的关键;本题难度较大.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 (选修模块3-3)
(选修模块3-3) 如图所示,在同一平面内放置的三条光滑平行足够长金属导轨a、b、c构成一个斜面,此斜面与水平面的夹角θ=30°,金属导轨相距均为d=1m,导轨ac间横跨一质量为m=0.8kg的金属棒MN,棒与每根导轨始终良好接触,棒的电阻r=1Ω,导轨的电阻忽略不计.在导轨bc间接一电阻恒为R=2Ω的灯泡,导轨ac间接一电压传感器(相当于理想电压表).整个装置放在磁感应强度B=2T的匀强磁场中,磁场方向垂直导轨平面向上.现对棒MN施加一沿斜面向下的拉力F使棒从静止开始运动,g取10m/s2.试求:(1)若施加的恒力F=2N,则金属棒达到稳定时速度为多少?(2)若施加的外力功率恒定,棒达到稳定时速度为4m/s,则此时外力的功率和电压传感器的读数分别为多少?(3)若施加的外力功率恒为P,经历时间为t,棒沿斜面轨道下滑距离为s、速度达到v3,则此过程中灯泡产生的热量为多少?
如图所示,在同一平面内放置的三条光滑平行足够长金属导轨a、b、c构成一个斜面,此斜面与水平面的夹角θ=30°,金属导轨相距均为d=1m,导轨ac间横跨一质量为m=0.8kg的金属棒MN,棒与每根导轨始终良好接触,棒的电阻r=1Ω,导轨的电阻忽略不计.在导轨bc间接一电阻恒为R=2Ω的灯泡,导轨ac间接一电压传感器(相当于理想电压表).整个装置放在磁感应强度B=2T的匀强磁场中,磁场方向垂直导轨平面向上.现对棒MN施加一沿斜面向下的拉力F使棒从静止开始运动,g取10m/s2.试求:(1)若施加的恒力F=2N,则金属棒达到稳定时速度为多少?(2)若施加的外力功率恒定,棒达到稳定时速度为4m/s,则此时外力的功率和电压传感器的读数分别为多少?(3)若施加的外力功率恒为P,经历时间为t,棒沿斜面轨道下滑距离为s、速度达到v3,则此过程中灯泡产生的热量为多少?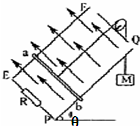 如图所示,无限长金属导轨EF、PQ固定在倾角为θ=30°的光滑绝缘斜面上,轨道间距L=1m,底部接入一阻值为R=0.4Ω的定值电阻,上端开口.垂直斜面向上的匀强磁场的磁感应强度B=2T.一质量为m=0.8kg的金属棒ab与导轨接触良好,ab与导轨间没有摩擦,ab连入导轨间的电阻r=0.1Ω,电路中其余电阻不计.现用一质量为M=2kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连.由静止释放M,不计空气阻力,当M下落高度h=2.0m时,ab开始匀速运动(运动中ab始终垂直导轨,并接触良好,g=10m/s2).求:
如图所示,无限长金属导轨EF、PQ固定在倾角为θ=30°的光滑绝缘斜面上,轨道间距L=1m,底部接入一阻值为R=0.4Ω的定值电阻,上端开口.垂直斜面向上的匀强磁场的磁感应强度B=2T.一质量为m=0.8kg的金属棒ab与导轨接触良好,ab与导轨间没有摩擦,ab连入导轨间的电阻r=0.1Ω,电路中其余电阻不计.现用一质量为M=2kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连.由静止释放M,不计空气阻力,当M下落高度h=2.0m时,ab开始匀速运动(运动中ab始终垂直导轨,并接触良好,g=10m/s2).求: