题目内容
6. 如图,在光滑水平面上放置一长木板,其上表面水平,左侧光滑,右侧OP段是长度为l=0.18m的粗糙面,木板左端上部固定一轻弹簧,右端用一不可伸长的细绳栓在墙上,细绳处于绷直状态,木板左边静止靠放着一个木球B,木板和木球的质量都为m=0.5kg,开始时,有一质量为M=4kg的滑块A,以大小v0=1.8m/s的初速度从木板上表面上光滑处向左运动,并压缩轻弹簧,当滑块的速度减小为原来的一半时,细绳突然被拉断(不计细绳断裂时的机械能损失),木板开始向左运动.
如图,在光滑水平面上放置一长木板,其上表面水平,左侧光滑,右侧OP段是长度为l=0.18m的粗糙面,木板左端上部固定一轻弹簧,右端用一不可伸长的细绳栓在墙上,细绳处于绷直状态,木板左边静止靠放着一个木球B,木板和木球的质量都为m=0.5kg,开始时,有一质量为M=4kg的滑块A,以大小v0=1.8m/s的初速度从木板上表面上光滑处向左运动,并压缩轻弹簧,当滑块的速度减小为原来的一半时,细绳突然被拉断(不计细绳断裂时的机械能损失),木板开始向左运动.(1)求木球B获得的最大速度?
(2)若滑块A恰好没有脱离木板,则滑块与木板间的动摩擦因数多大?
(3)若滑块A最后恰好没有脱离木板,则当滑块运动到木板右端时,木球B与木板之间的间距多大?
分析 (1)在剪短绳后,当弹簧达到原长时物体B具有最大速度,在此过程中利用动量定理和能量守恒即可求得
(2)当物体A在OP间运动时,A做加速运动,木板做减速运动,利用牛顿第二定律求得各自的加速度,再结合运动学公式即可求得摩擦因数;
(3)利用运动学公式分别求的木板和球的位移即可
解答 解:(1)当弹簧再次达到原长时小球B获得最大速度,
在整个过程中动量守恒,选向左为正方则
$M•\frac{{v}_{0}}{2}=Mv′+2mv″$
整个过程中能量守恒$\frac{1}{2}{Mv}_{0}^{2}=\frac{1}{2}Mv{′}^{2}+\frac{1}{2}•2mv{″}^{2}$
联立解得v′=0,v″=3.6m/s
(2)物体A在OP间运动时,木板的加速度为${a}_{1}=\frac{μMg}{m}=8μg$
物体A的加速度为${a}_{2}=\frac{μMg}{M}=μg$
当两者达到相同速度时v″-a1t=a2t
解得$t=\frac{0.6}{μg}$
两者的位移之差为l=$v″t-\frac{1}{2}{a}_{1}{t}^{2}-\frac{1}{2}{a}_{2}{t}^{2}$
联立解得μ=0.3
(3)由(2)可知,达到相同速度所需时间为t=0.2s
木板在0.2s内前进的位移为$x=v″t-\frac{1}{2}{a}_{1}{t}^{2}=0.24m$
球前进的位移为x′=v″t=7.2m
木球B与木板之间的间距为△x=x′-x=0.48m
答:(1)木球B获得的最大速度为3.6m/s
(2)若滑块A恰好没有脱离木板,则滑块与木板间的动摩擦因数为0.3
(3)若滑块A最后恰好没有脱离木板,则当滑块运动到木板右端时,木球B与木板之间的间距为0.48m
点评 本题主要考查了牛顿第二定律与动量守恒、能量守恒,考查的知识点较多,综合性较强

 金博士一点全通系列答案
金博士一点全通系列答案| A. | 火星和地球的质量之比 | |
| B. | 火星和地球到太阳的距离之比 | |
| C. | 火星和太阳的质量之比 | |
| D. | 火星和地球绕太阳运行速度大小之比 |
 如图所示,MN,PQ是水平面内的两条光滑金属导轨,其电阻不计,金属棒ab垂直放置在两导轨上,匀强磁场垂直导轨平面.将ab棒由图示位置分别以速度v1和v2匀速拉到a′b′位置,比较这两个过程,下列说法正确的是( )
如图所示,MN,PQ是水平面内的两条光滑金属导轨,其电阻不计,金属棒ab垂直放置在两导轨上,匀强磁场垂直导轨平面.将ab棒由图示位置分别以速度v1和v2匀速拉到a′b′位置,比较这两个过程,下列说法正确的是( )| A. | 若v1>v2,两次通过棒a,b截面的电量关系是q1>q2 | |
| B. | 若v1>v2,两次拉力关系是F1>F2 | |
| C. | 若v1>2v2,两次拉力做功关系是W1=W2 |
 如图所示,光电管的阴极用极限波长λ0=5000?的钠制成.用波长λ=3000?的紫外线照射阴极,光电管阳极A和阴极K之间的电势差U=2.1V,饱和光电流的值I=0.56μA (当阴极K发射的电子全部到达阳极A时,电路中的电流达到最大值,称为饱和光电流).
如图所示,光电管的阴极用极限波长λ0=5000?的钠制成.用波长λ=3000?的紫外线照射阴极,光电管阳极A和阴极K之间的电势差U=2.1V,饱和光电流的值I=0.56μA (当阴极K发射的电子全部到达阳极A时,电路中的电流达到最大值,称为饱和光电流).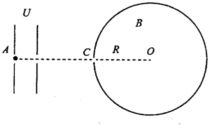 在光滑绝缘的水平面上,左侧平行极板间有水平方向匀强电场,右侧圆筒内有竖直方向匀强磁场,磁感应强度大小为B,俯视图如图所示,圆的圆心为O点,半径大小为R,一质量为m、电荷量大小为q的带电小球(可视为质点),初速位置在A点,现由静止经电场加速后从C孔沿直径射入磁场区域,粒子和圆筒壁的碰撞没有动能和电荷量损失,B、R、m、q为已知量,圆筒仅有一个出入口C.
在光滑绝缘的水平面上,左侧平行极板间有水平方向匀强电场,右侧圆筒内有竖直方向匀强磁场,磁感应强度大小为B,俯视图如图所示,圆的圆心为O点,半径大小为R,一质量为m、电荷量大小为q的带电小球(可视为质点),初速位置在A点,现由静止经电场加速后从C孔沿直径射入磁场区域,粒子和圆筒壁的碰撞没有动能和电荷量损失,B、R、m、q为已知量,圆筒仅有一个出入口C.
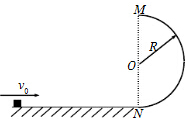 如图,质量m=1.0kg的物体(可视为质点)以v0=10m/s的初速度从水平面的某点向右运动并冲上半径R=1.0m的竖直光滑半圆环,物体与水平面间的动摩擦因数μ=0.5.求:
如图,质量m=1.0kg的物体(可视为质点)以v0=10m/s的初速度从水平面的某点向右运动并冲上半径R=1.0m的竖直光滑半圆环,物体与水平面间的动摩擦因数μ=0.5.求: