题目内容
8. 如图所示,边长为2l的正方形虚线框内有垂直于纸面向里的匀强磁场,磁感应强度大小为B.一个由某种材料做成的边长为l、粗细均匀的正方形导线框abcd所在平面与磁场方向垂直;导线框、虚线框的对角线重合,导线框各边的电阻大小均为R.在导线框从图示位置开始以恒定速度”沿对角线方向进入磁场,到整个导线框离开磁场区域的过程中,下列说法正确的是( )
如图所示,边长为2l的正方形虚线框内有垂直于纸面向里的匀强磁场,磁感应强度大小为B.一个由某种材料做成的边长为l、粗细均匀的正方形导线框abcd所在平面与磁场方向垂直;导线框、虚线框的对角线重合,导线框各边的电阻大小均为R.在导线框从图示位置开始以恒定速度”沿对角线方向进入磁场,到整个导线框离开磁场区域的过程中,下列说法正确的是( )| A. | 导线框进入磁场区域的过程中有向外扩张的趋势 | |
| B. | 导线框中有感应电流的时间为$\frac{2l}{v}$ | |
| C. | 导线框的bd对角线有一半进入磁场时,整个导线框所受安培力大小为$\frac{{B}^{2}{l}^{2}v}{2R}$ | |
| D. | 导线框的bd对角线有一半进入磁场时,导线框a,c两点间的电压为$\frac{\sqrt{2}Blv}{4}$ |
分析 根据楞次定律判断感应电流的方向;当磁通量变化时,线框中将产生感应电流;确定出线框有效的切割长度,由公式E=BLv求出感应电动势,由欧姆定律求出感应电流,由F=BIL求出安培力,由串联电路的特点求解a、c间的电压.
解答 解:
A、导线框进入磁场区域时磁通量增加,根据楞次定律判断得知产生逆时针方向的感应电流,由于磁通量增大,故线圈由收缩的趋势;故A错误.
B、当线框进入和离开磁场时磁通量变化,才有感应电流产生,所以有感应电流的时间为 t=$\frac{s}{v}$=$\frac{2\sqrt{2}L}{v}$,故B错误.
C、D、导线框的bd对角线有一半进入磁场时,线框有效的切割长度为:l=$\frac{\sqrt{2}}{2}$L,
产生的感应电动势为:E=Blv=$\frac{\sqrt{2}}{2}$BLv,
感应电流为:I=$\frac{E}{4R}$=$\frac{\sqrt{2}BLv}{8R}$,
整个导线框所受安培力大小为:F=BIl=B•$\frac{\sqrt{2}BLv}{8R}$•$\frac{\sqrt{2}}{2}$L=$\frac{{B}^{2}{L}^{2}v}{8R}$;
导线框a、c两点间的电压为:U=I•2R=$\frac{{\sqrt{2}BLυ}}{4}$,故C错误,D正确.
故选:D.
点评 本题关键要理解“有效”二字,知道感应电动势公式E=Blv中l是有效的切割长度,安培力公式F=BIl,l也是有效长度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16. 如图所示的电路中,开关闭合后,水平放置的平行板电容器中有一个带电液滴恰好处于静止状态,在保持开关闭合的情况下,将滑动变阻器的滑片P向下滑动,则( )
如图所示的电路中,开关闭合后,水平放置的平行板电容器中有一个带电液滴恰好处于静止状态,在保持开关闭合的情况下,将滑动变阻器的滑片P向下滑动,则( )
 如图所示的电路中,开关闭合后,水平放置的平行板电容器中有一个带电液滴恰好处于静止状态,在保持开关闭合的情况下,将滑动变阻器的滑片P向下滑动,则( )
如图所示的电路中,开关闭合后,水平放置的平行板电容器中有一个带电液滴恰好处于静止状态,在保持开关闭合的情况下,将滑动变阻器的滑片P向下滑动,则( )| A. | 通过滑动变阻器的电流减小 | B. | 带电液滴向上运动 | ||
| C. | 带电液滴向下运动 | D. | 电容器的带电荷量将增加 |
3. 如图所示,理想变压器原、副线圈的匝数比为n1:n2=10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为μ1=220$\sqrt{2}$sin100πt(V),开始时,单刀双掷开关与a连接,下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比为n1:n2=10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为μ1=220$\sqrt{2}$sin100πt(V),开始时,单刀双掷开关与a连接,下列说法中正确的是( )
 如图所示,理想变压器原、副线圈的匝数比为n1:n2=10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为μ1=220$\sqrt{2}$sin100πt(V),开始时,单刀双掷开关与a连接,下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比为n1:n2=10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为μ1=220$\sqrt{2}$sin100πt(V),开始时,单刀双掷开关与a连接,下列说法中正确的是( )| A. | t=$\frac{1}{200}$时,cd间电压的瞬时值为220V | |
| B. | t=$\frac{1}{200}$ 时,电压表的示数为22V | |
| C. | 若将滑动变阻器的滑片向上移,电流变和电压表的示数都变小 | |
| D. | 当单刀双掷开关由a拨向b时,电压表和电流表的示数均变小 |
18.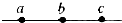 如图所示,沿波的传播方向上有间距均为1m的质点a、b、c,静止在各自的平衡位置,一列横波以1m/s的速度水平向右传播,t=0时质点a开始由平衡位置向上运动,t=1s时质点a第一次到达最高点.在8s<t<9s这段时间内质点c的状态是( )
如图所示,沿波的传播方向上有间距均为1m的质点a、b、c,静止在各自的平衡位置,一列横波以1m/s的速度水平向右传播,t=0时质点a开始由平衡位置向上运动,t=1s时质点a第一次到达最高点.在8s<t<9s这段时间内质点c的状态是( )
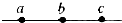 如图所示,沿波的传播方向上有间距均为1m的质点a、b、c,静止在各自的平衡位置,一列横波以1m/s的速度水平向右传播,t=0时质点a开始由平衡位置向上运动,t=1s时质点a第一次到达最高点.在8s<t<9s这段时间内质点c的状态是( )
如图所示,沿波的传播方向上有间距均为1m的质点a、b、c,静止在各自的平衡位置,一列横波以1m/s的速度水平向右传播,t=0时质点a开始由平衡位置向上运动,t=1s时质点a第一次到达最高点.在8s<t<9s这段时间内质点c的状态是( )| A. | 速度逐渐增大 | B. | 加速度逐渐增大 | ||
| C. | 一直在向上运动 | D. | 先向下后向上运动 |
 如图所示是一列沿x轴正方向传播的简谐横波在t=0时刻的图象,波的传播速度v=2m/s,试回答下列问题:
如图所示是一列沿x轴正方向传播的简谐横波在t=0时刻的图象,波的传播速度v=2m/s,试回答下列问题:
 如图甲所示,物体A、B的质量分别是4kg和8kg,由轻弹簧连接,放在光滑的水平面上,物体B左侧与竖直墙壁相接触,另有一个物体C水平向左运动,在t=5s时与物体A相碰度立即与A具有相同的速度一起向左运动,物块C的速度一时间图象如图乙所示,求:
如图甲所示,物体A、B的质量分别是4kg和8kg,由轻弹簧连接,放在光滑的水平面上,物体B左侧与竖直墙壁相接触,另有一个物体C水平向左运动,在t=5s时与物体A相碰度立即与A具有相同的速度一起向左运动,物块C的速度一时间图象如图乙所示,求: