题目内容
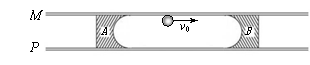
（18分）固定在水平面上的无限长的两根直导轨MN、PQ，内部左右两边各放置完全相同滑块A、B，滑块的凹槽半径是R，滑块的宽度为2R，比导轨间距略小，两滑块可以沿导轨滑行，如图所示，不计一切摩擦。现有半径r(r<<R)的金属小球以水平初速度v0冲向右滑块，从滑块的一侧半圆形槽口边缘进入。已知金属小球的质量为m，A、B滑块的质量均为km，其中k=1、2、3……，整个运动过程中无机械能损失。求:
（1）当金属小球第一次滑离B滑块时，金属小球的速度是多大？
（2）若小球和B滑块最少能碰撞2次，求k的取值范围？
解：（1）设滑离B滑块时，小球和B滑块的速度分别为
，由动量守恒可得
（2分）
由机械能守恒可得
（2分）
联立解得小球速度为
（2分）
B滑块速度为
（2分）
（2）设滑离A滑块时，小球和A滑块的速度分别为
和
，由动量守恒可得
（1分）
由机械能守恒可得
（1分）
联立解得小球的速度
（2分）
若小球和B滑块最少能碰撞2次，则必有
＞
（2分）
化简
-4k-1＞ 0 （1分）
解得K＞ 2+
（1分）
故k=5、6、7……（2分）
练习册系列答案
相关题目
