题目内容
7. 如图所示,光滑水平轨道上放置足够长的木板A(上表面粗糙)和滑块C,滑块B置于A的左端,已知mA=1kg、mB=3kg.开始时C静止,A、B一起以v0的速度匀速向右运动,A与C发生碰撞(时间极短)后,C向右运动,碰撞过程无机械能损失,最终A、B和C速度相等.求C的质量.
如图所示,光滑水平轨道上放置足够长的木板A(上表面粗糙)和滑块C,滑块B置于A的左端,已知mA=1kg、mB=3kg.开始时C静止,A、B一起以v0的速度匀速向右运动,A与C发生碰撞(时间极短)后,C向右运动,碰撞过程无机械能损失,最终A、B和C速度相等.求C的质量.
分析 A与C碰撞过程动量守恒列出等式,A与B在摩擦力作用下达到共同速度,由动量守恒定律列出等式,最终A、B和C速度相等,联立方程即可求解.
解答 解:因碰撞时间极短,A与C碰撞过程动量守恒,设碰撞后瞬间A的速度大小为vA,C的速度大小为vC,以向右为正方向,由动量守恒定律及机械能守恒得:
mAv0=mAvA+mCvC…①
$\frac{1}{2}$mAv02=$\frac{1}{2}$mAvA2+$\frac{1}{2}$mCvC2…②
A与B在摩擦力作用下达到共同速度,设共同速度为vAB,由动量守恒定律得:
mAvA+mBv0=(mA+mB) vAB…③
最终A、B和C速度相等,应满足:vAB=vC …④
联立①②③④式解得:mC=2kg
答:C的质量为2kg.
点评 分析物体的运动过程,选择不同的系统作为研究对象,运用动量守恒定律求解,难度不大,所以基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20. 如图,倾斜平行导轨处在垂直导轨平面的匀强磁场中,横跨导轨静止放置一根金属杆ab(与导轨垂直),ab与导轨以及上端的电阻R组成一闭合回路.当匀强磁场的磁感强度由0均匀增大且杆仍能保持静止时,ab杆受到的静摩擦力的大小( )
如图,倾斜平行导轨处在垂直导轨平面的匀强磁场中,横跨导轨静止放置一根金属杆ab(与导轨垂直),ab与导轨以及上端的电阻R组成一闭合回路.当匀强磁场的磁感强度由0均匀增大且杆仍能保持静止时,ab杆受到的静摩擦力的大小( )
 如图,倾斜平行导轨处在垂直导轨平面的匀强磁场中,横跨导轨静止放置一根金属杆ab(与导轨垂直),ab与导轨以及上端的电阻R组成一闭合回路.当匀强磁场的磁感强度由0均匀增大且杆仍能保持静止时,ab杆受到的静摩擦力的大小( )
如图,倾斜平行导轨处在垂直导轨平面的匀强磁场中,横跨导轨静止放置一根金属杆ab(与导轨垂直),ab与导轨以及上端的电阻R组成一闭合回路.当匀强磁场的磁感强度由0均匀增大且杆仍能保持静止时,ab杆受到的静摩擦力的大小( )| A. | 逐渐增大 | B. | 先逐渐减小,后逐渐增大 | ||
| C. | 逐渐减小 | D. | 先逐渐增大,后逐渐减小 |
1.(多选)关于万有引力,下列说法不正确的是( )
| A. | 牛顿正式提出了万有引力定律并利用扭秤测出了引力常量 | |
| B. | 测量引力常量的扭秤实验涉及的物理思想方法是微小量放大法 | |
| C. | 根据万有引力公式可知,假设地球球心有一物体,则它和地球之间的万有引力会趋于无穷大 | |
| D. | 德国天文学家开普勒提出开普勒三大定律 |
2.图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x=1m处的质点,Q是平衡位置为x=4m处的质点,图乙为质点Q的振动图象,则( )


| A. | 波向-x方向传播 | |
| B. | 该波的波速为40m/s | |
| C. | t=0.10时刻质点P正向平衡位置运动 | |
| D. | t=0.075s时刻质点P运动至平衡位置 |
12.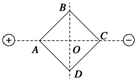 如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )
如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )
 如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )
如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )| A. | A点的电场强度等于B点的电场强度 | |
| B. | B、D两点的电场强度及电势均相同 | |
| C. | 一电子由B点沿B→C→D路径移至D点,电势能先减小后增大 | |
| D. | 一电子由C点沿C→O→A路径移至A点,电场力对其先做负功后做正功 |
19. 如图所示,桌面离地高度为h,质量为m的小球,从离桌面H高处由静止下落.若以桌面为参考平面,那么小球落地时的重力势能及整个下落过程中重力势能的变化分别为( )
如图所示,桌面离地高度为h,质量为m的小球,从离桌面H高处由静止下落.若以桌面为参考平面,那么小球落地时的重力势能及整个下落过程中重力势能的变化分别为( )
 如图所示,桌面离地高度为h,质量为m的小球,从离桌面H高处由静止下落.若以桌面为参考平面,那么小球落地时的重力势能及整个下落过程中重力势能的变化分别为( )
如图所示,桌面离地高度为h,质量为m的小球,从离桌面H高处由静止下落.若以桌面为参考平面,那么小球落地时的重力势能及整个下落过程中重力势能的变化分别为( )| A. | mgh,减少mg(H-h) | B. | mgh,增加mg(H+h) | C. | -mgh,增加mg(H-h) | D. | -mgh,减少mg(H+h) |
16. 如图,固定有滑圆弧轨道的小车A静止在光的水平面上,轨道足够长,其下部分水平,有一小滑块B以某水平初速度滑上小车,滑轮不从圆弧上端滑出,则滑块B在车上运动的过程中( )
如图,固定有滑圆弧轨道的小车A静止在光的水平面上,轨道足够长,其下部分水平,有一小滑块B以某水平初速度滑上小车,滑轮不从圆弧上端滑出,则滑块B在车上运动的过程中( )
 如图,固定有滑圆弧轨道的小车A静止在光的水平面上,轨道足够长,其下部分水平,有一小滑块B以某水平初速度滑上小车,滑轮不从圆弧上端滑出,则滑块B在车上运动的过程中( )
如图,固定有滑圆弧轨道的小车A静止在光的水平面上,轨道足够长,其下部分水平,有一小滑块B以某水平初速度滑上小车,滑轮不从圆弧上端滑出,则滑块B在车上运动的过程中( )| A. | 当滑块上升到最大高度时,滑块的速度为零 | |
| B. | 滑块运动过程中机械能守恒 | |
| C. | 滑块离开小车时的速度与滑上小车时的速度大小相等 | |
| D. | 滑块B在小车上运动的过程中,滑块与小车组成的系统动量不守恒 |
 如图所示,在内壁光滑的平底玻璃管内,装有一质量为10g的小球(可视为质点),将玻璃管开口端封闭后安装在转轴O上,转轴到管底的距离为25cm,让玻璃管在竖直面内匀速转动,求:
如图所示,在内壁光滑的平底玻璃管内,装有一质量为10g的小球(可视为质点),将玻璃管开口端封闭后安装在转轴O上,转轴到管底的距离为25cm,让玻璃管在竖直面内匀速转动,求: