题目内容
13.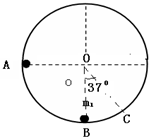 如图,内壁光滑的半径为R的圆形轨道,固定在竖直平面内,质量为m1的小球静止在轨道最低点,另一质量为m2的小球(两小球均可视为质点)从内壁上与圆心0等高处由静止释放,到最低点时与m1发生正碰并结合为一整体P,整体P能上升到与C处,OC与竖直夹角为37°.求
如图,内壁光滑的半径为R的圆形轨道,固定在竖直平面内,质量为m1的小球静止在轨道最低点,另一质量为m2的小球(两小球均可视为质点)从内壁上与圆心0等高处由静止释放,到最低点时与m1发生正碰并结合为一整体P,整体P能上升到与C处,OC与竖直夹角为37°.求(1)整体P在最低点处的速度大小.
(2)m2和m1的比值.
分析 (1)P从最低点B到C点过程机械能守恒,由机械能守恒定律可以求出P在最低点的速度.
(2)m2从A到B过程机械能守恒,两球碰撞过程动量守恒,应用机械能守恒定律与动量守恒定律可以求出两球的质量之比.
解答 解:(1)P从B运动到C过程机械能守恒,由机械能守恒定律得:
$\frac{1}{2}$(m1+m2)v2=(m1+m2)gR(1-cos37°),解得:v=$\sqrt{\frac{2}{5}gR}$;
(2)m2从A运动到B的过程中机械能守恒,由机械能守恒定律得:m2gR=$\frac{1}{2}$m2v02,
两球碰撞过程系统动量守恒,以水平向右为正方向,
由动量守恒定律得:m2v0=(m1+m2)v,解得:$\frac{{m}_{1}}{{m}_{2}}$=$\sqrt{5}$-1;
答:(1)整体P在最低点处的速度大小为$\sqrt{\frac{2}{5}gR}$.
(2)m2和m1的比值为$\sqrt{5}$-1.
点评 本题解题的关键是对两个小球运动情况的分析,知道小球做什么运动,并能结合机械能守恒、动量守恒等关系解题,难度比较大.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
4.下列说法正确的是( )
| A. | 当水波通过障碍物时,若障碍的尺寸与波长差不多,或比波长大的多时,将发生明显的衍射现象 | |
| B. | 单摆在周期性外力作用下做受迫振动,其振动周期与单摆的摆长无关 | |
| C. | 光纤通信的工作原理是全反射,光纤通信具有容量大、抗干扰性强等优点 | |
| D. | 拍摄玻璃橱窗内的物品时,要在镜头前加装一个偏振片以增加透射光的强度 |
8. 如图所示为运送粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,(设最大静摩擦力等于滑动摩擦力)以下说法正确的是( )
如图所示为运送粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,(设最大静摩擦力等于滑动摩擦力)以下说法正确的是( )
 如图所示为运送粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,(设最大静摩擦力等于滑动摩擦力)以下说法正确的是( )
如图所示为运送粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,(设最大静摩擦力等于滑动摩擦力)以下说法正确的是( )| A. | 粮袋到达B点的速度不可能大于v | |
| B. | 粮袋开始运动的加速度为g(sinθ-μcosθ),若L足够大,则以后将以速度v做匀速运动 | |
| C. | 若μ<tanθ,则粮袋从A到B一直做加速运动 | |
| D. | 不论μ大小如何,粮袋从A到B一直做匀加速运动,且a>gsinθ |
18. 如图所示,在直线l上A、B两点各固定电量均为Q的正电荷,O为AB的中点,C、D两点关于A点对称,C、D两点的场强大小分别为EC、ED,电势分别为φC、φD,则以下说法正确的是( )
如图所示,在直线l上A、B两点各固定电量均为Q的正电荷,O为AB的中点,C、D两点关于A点对称,C、D两点的场强大小分别为EC、ED,电势分别为φC、φD,则以下说法正确的是( )
 如图所示,在直线l上A、B两点各固定电量均为Q的正电荷,O为AB的中点,C、D两点关于A点对称,C、D两点的场强大小分别为EC、ED,电势分别为φC、φD,则以下说法正确的是( )
如图所示,在直线l上A、B两点各固定电量均为Q的正电荷,O为AB的中点,C、D两点关于A点对称,C、D两点的场强大小分别为EC、ED,电势分别为φC、φD,则以下说法正确的是( )| A. | EC>ED,φC>φD | |
| B. | EC<ED,φC>φD | |
| C. | 在直线l上与D点电势相等的点除D点外可能还有3个点 | |
| D. | 将一负电荷从C点移到D点其电势能增大 |
5.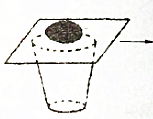 如图所示,一只杯子固定在水平桌面上,将一块薄纸板盖在杯口并在纸板上放一枚鸡蛋,现用水平向右的拉力将纸板快速抽出,鸡蛋(水平移动距离很小,几乎看不到)掉入杯中,这就是惯性演示.已知鸡蛋(可视为质点)中心离纸板左端的距离为d,鸡蛋和纸板的质量分别为m和2m,所有接触面的动摩擦因数均为μ,重力加速度为g,若鸡蛋移动的距离不超过$\frac{d}{10}$就能保证实验成功,则所需拉力的最小值为( )
如图所示,一只杯子固定在水平桌面上,将一块薄纸板盖在杯口并在纸板上放一枚鸡蛋,现用水平向右的拉力将纸板快速抽出,鸡蛋(水平移动距离很小,几乎看不到)掉入杯中,这就是惯性演示.已知鸡蛋(可视为质点)中心离纸板左端的距离为d,鸡蛋和纸板的质量分别为m和2m,所有接触面的动摩擦因数均为μ,重力加速度为g,若鸡蛋移动的距离不超过$\frac{d}{10}$就能保证实验成功,则所需拉力的最小值为( )
 如图所示,一只杯子固定在水平桌面上,将一块薄纸板盖在杯口并在纸板上放一枚鸡蛋,现用水平向右的拉力将纸板快速抽出,鸡蛋(水平移动距离很小,几乎看不到)掉入杯中,这就是惯性演示.已知鸡蛋(可视为质点)中心离纸板左端的距离为d,鸡蛋和纸板的质量分别为m和2m,所有接触面的动摩擦因数均为μ,重力加速度为g,若鸡蛋移动的距离不超过$\frac{d}{10}$就能保证实验成功,则所需拉力的最小值为( )
如图所示,一只杯子固定在水平桌面上,将一块薄纸板盖在杯口并在纸板上放一枚鸡蛋,现用水平向右的拉力将纸板快速抽出,鸡蛋(水平移动距离很小,几乎看不到)掉入杯中,这就是惯性演示.已知鸡蛋(可视为质点)中心离纸板左端的距离为d,鸡蛋和纸板的质量分别为m和2m,所有接触面的动摩擦因数均为μ,重力加速度为g,若鸡蛋移动的距离不超过$\frac{d}{10}$就能保证实验成功,则所需拉力的最小值为( )| A. | 3μmg | B. | 26μmg | C. | 12μmg | D. | 15μmg |
10. 我国月球探测活动的第一步“绕月”工程和第二步“落月”工程已按计划在2013年以前顺利完成.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时点火变轨进入椭圆转移轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,则下列判断正确的是( )
我国月球探测活动的第一步“绕月”工程和第二步“落月”工程已按计划在2013年以前顺利完成.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时点火变轨进入椭圆转移轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,则下列判断正确的是( )
 我国月球探测活动的第一步“绕月”工程和第二步“落月”工程已按计划在2013年以前顺利完成.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时点火变轨进入椭圆转移轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,则下列判断正确的是( )
我国月球探测活动的第一步“绕月”工程和第二步“落月”工程已按计划在2013年以前顺利完成.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时点火变轨进入椭圆转移轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,则下列判断正确的是( )| A. | 飞船在轨道Ⅰ上的运行速率v=$\frac{{\sqrt{{g_0}R}}}{2}$ | |
| B. | 飞船在A点处点火变轨时,动能和机械能都增大 | |
| C. | 飞船在转移轨道上从A到B运行的过程中机械能不变,引力势能增大 | |
| D. | 飞船在轨道Ⅲ绕月球运动一周所需的时间T=π$\sqrt{\frac{R}{g_0}}$ |
11.如图甲所示变压器可视为理想变压器,其原线圈输入如图乙所示的交变电压,铭牌上标注“22V、11W”的小电动机刚好正常工作,图中A、V为理想交流电流表和电压表.下列说法正确的是( )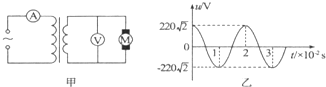

| A. | 通过小电动机电流的频率为50Hz | |
| B. | 原线圈输入的交变电压的瞬时值表达式为u=220cos50πt(V) | |
| C. | 电流表的示数为0.05A | |
| D. | 如果电动机转子突然被卡住不转,变压器的输入功率减小 |
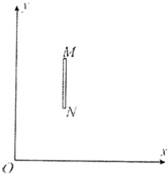 如图所示,在x≥0的区域内存在与x0y平面垂直的匀强磁场,磁感应强度的大小为B,方向垂直于纸面向里.假设一束初速度为零的质量为m、带电荷量为q的正离子,经过加速电场加速后从O点沿x轴正方向进入匀强磁场区域.有一块厚度不计、高度为d的金属板竖直放置在磁场中,截面如图,M、N分别为金属板截面的上、下端点,M点的坐标为(d,2d),N点的坐标为(d,d).正离子的重力不计.
如图所示,在x≥0的区域内存在与x0y平面垂直的匀强磁场,磁感应强度的大小为B,方向垂直于纸面向里.假设一束初速度为零的质量为m、带电荷量为q的正离子,经过加速电场加速后从O点沿x轴正方向进入匀强磁场区域.有一块厚度不计、高度为d的金属板竖直放置在磁场中,截面如图,M、N分别为金属板截面的上、下端点,M点的坐标为(d,2d),N点的坐标为(d,d).正离子的重力不计. 如图所示,直角玻璃三棱镜置于空气中,已知∠A=60°,∠C=90°,一束极细的光于AC边的中点D垂直AC面入射,AD=a,棱镜的折射率n=$\sqrt{2}$.求:
如图所示,直角玻璃三棱镜置于空气中,已知∠A=60°,∠C=90°,一束极细的光于AC边的中点D垂直AC面入射,AD=a,棱镜的折射率n=$\sqrt{2}$.求: