题目内容
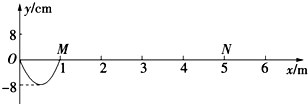
3.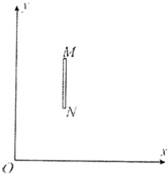 如图所示,在x≥0的区域内存在与x0y平面垂直的匀强磁场,磁感应强度的大小为B,方向垂直于纸面向里.假设一束初速度为零的质量为m、带电荷量为q的正离子,经过加速电场加速后从O点沿x轴正方向进入匀强磁场区域.有一块厚度不计、高度为d的金属板竖直放置在磁场中,截面如图,M、N分别为金属板截面的上、下端点,M点的坐标为(d,2d),N点的坐标为(d,d).正离子的重力不计.
如图所示,在x≥0的区域内存在与x0y平面垂直的匀强磁场,磁感应强度的大小为B,方向垂直于纸面向里.假设一束初速度为零的质量为m、带电荷量为q的正离子,经过加速电场加速后从O点沿x轴正方向进入匀强磁场区域.有一块厚度不计、高度为d的金属板竖直放置在磁场中,截面如图,M、N分别为金属板截面的上、下端点,M点的坐标为(d,2d),N点的坐标为(d,d).正离子的重力不计.(1)加速电场的电压在什么范围内,进入磁场的离子才能全部打在金属板上?
(2)求打在金属板上的离子在磁场中运动的最短时间与最长时间的比值.(sin37°=0.6,cos37°=0.8)
分析 求出恰好打到N点时的半径,在求出恰好打到M点的半径,中间的数据就是所求的电压范围;分别求出打到M点时的最长时间和打到N点时的最短时间,然后求比值即可.
解答 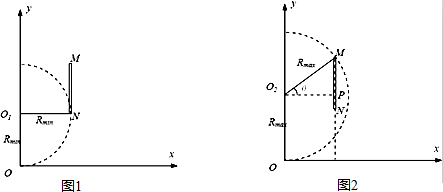 解:(1)设加速电压为U,正离子初速度为零,经过加速电场加速,根据动能定理得:
解:(1)设加速电压为U,正离子初速度为零,经过加速电场加速,根据动能定理得:
qU=$\frac{1}{2}m{v}^{2}$
正离子在磁场中做匀速圆周运动,洛伦兹力提供向心力:
qvB=$\frac{m{v}^{2}}{R}$
R=$\frac{\sqrt{2mqU}}{qB}$
当加速电压较小时,离子在磁场中做匀速圆周运动的半径较小,当离子恰好打到金属板下端点N点时,圆周运动的半径最小为Rmin,如图1
根据几何知识可以判断Rmin=d
故:Umin=$\frac{q{B}^{2}{d}^{2}}{2m}$
当加速电压较大时,离子在磁场中做匀速圆周运动的半径较大,当离子恰好打到金属板上端点M点时,圆周运动的半径最大为Rmax,如图2
根据几何知识判断:Rmax2=d2+(2d-Rmin)2
解得Rmax=$\frac{5}{4}$d
所以Umax=$\frac{25q{B}^{2}{d}^{2}}{32m}$
所以离子能全部打在金属板上,加速电压的取值范围为:$\frac{q{B}^{2}{d}^{2}}{2m}$≤U≤$\frac{25q{B}^{2}{d}^{2}}{32m}$
(2)设离子在磁场中做匀速圆周运动的周期为T,根据圆周运动规律得:
T=$\frac{2πR}{v}$…①
又qvB=$\frac{m{v}^{2}}{R}$…②
联立①②解得T=$\frac{2πm}{qB}$
离子在磁场中做匀速圆周运动的周期与加速电压无关.
离子在图1中所示的轨迹中运动时间最短为
tmin=$\frac{1}{4}$T
离子在图2所示的轨迹中运动时间最长为:
tmax=$\frac{90°+θ}{360°}$
根据几何知识:cosθ=$\frac{d}{{r}_{max}}=\frac{4}{5}$
则:θ=37°
所以$\frac{{t}_{min}}{{t}_{max}}=\frac{90}{127}$
答:(1)加速电场的电压在为:$\frac{q{B}^{2}{d}^{2}}{2m}$≤U≤$\frac{25q{B}^{2}{d}^{2}}{32m}$范围内,进入磁场的离子才能全部打在金属板上,
(2)打在金属板上的离子在磁场中运动的最短时间与最长时间的比值为$\frac{90}{127}$.
点评 此题考查离子在匀强磁场中的运动情况,属于高考常见题目,要加强联系,难度适中.

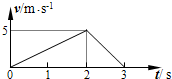
| A. | 位移大小相等 | B. | 平均速度相等 | C. | 速度变化相同 | D. | 运动方向相同 |
| A. | 英国科学家伽利略在研究物体变速运动规律时,做了著名的“斜面实验” | |
| B. | 法拉第对电磁感应现象的研究作出了突出的贡献,他首先总结出了判断感应电流方向的规律 | |
| C. | 牛顿对物理学作出了划时代的贡献,是动力学的奠基人,所以在力学单位制中,力的单位牛顿是基本单位 | |
| D. | 元电荷e的数值最早是由物理学家密立根测得的 |
 一个闭合回路由两部分组成,如图所示,右侧是电阻为r的圆形导线,置于竖直方向均匀变化的磁场B1中;左侧是光滑的倾角为θ的平行导轨,宽度为d,其电阻不计.置于磁感应强度为B2的竖直向上的匀强磁场中,一个质量为m、电阻为R的导体棒此时恰好能静止在导轨上,分析下述判断正确的有( )
一个闭合回路由两部分组成,如图所示,右侧是电阻为r的圆形导线,置于竖直方向均匀变化的磁场B1中;左侧是光滑的倾角为θ的平行导轨,宽度为d,其电阻不计.置于磁感应强度为B2的竖直向上的匀强磁场中,一个质量为m、电阻为R的导体棒此时恰好能静止在导轨上,分析下述判断正确的有( )| A. | 圆形线圈中的磁场可以是向上均匀减弱 | |
| B. | 导体棒ab受到的安培力大小为mgsinθ | |
| C. | 回路中的感应电流为$\frac{mgtanθ}{{B}_{2}d}$ | |
| D. | 圆形导线中的电热功率为$\frac{{m}^{2}{g}^{2}rta{n}^{2}θ}{{{B}_{2}}^{2}{d}^{2}}$ |
 如图所示,两个半径为R的四分之一圆弧构成的光滑细管道ABC竖直放置,且固定在光滑水平面上,圆心连线O1O2水平.轻弹簧左端固定在竖直挡板上,右端与质量为m的小球接触(不拴接,小球的直径略小于管道内径),开始时弹簧处于锁定状态,具有一定的弹性势能,重力加速度为g.解除锁定,小球离开弹簧后进入管道.
如图所示,两个半径为R的四分之一圆弧构成的光滑细管道ABC竖直放置,且固定在光滑水平面上,圆心连线O1O2水平.轻弹簧左端固定在竖直挡板上,右端与质量为m的小球接触(不拴接,小球的直径略小于管道内径),开始时弹簧处于锁定状态,具有一定的弹性势能,重力加速度为g.解除锁定,小球离开弹簧后进入管道.

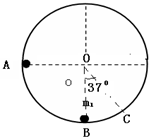 如图,内壁光滑的半径为R的圆形轨道,固定在竖直平面内,质量为m1的小球静止在轨道最低点,另一质量为m2的小球(两小球均可视为质点)从内壁上与圆心0等高处由静止释放,到最低点时与m1发生正碰并结合为一整体P,整体P能上升到与C处,OC与竖直夹角为37°.求
如图,内壁光滑的半径为R的圆形轨道,固定在竖直平面内,质量为m1的小球静止在轨道最低点,另一质量为m2的小球(两小球均可视为质点)从内壁上与圆心0等高处由静止释放,到最低点时与m1发生正碰并结合为一整体P,整体P能上升到与C处,OC与竖直夹角为37°.求