题目内容
8.某实验小组用如图1所示装置做“验证机械能守恒定律”实验.(1)实验中除了打点计时器,还必须用到的测量工具为刻度尺.
(2)在实验操作和数据处理过程巾,下列做法必须有的是D.
A.用天平测出重物的质量
B.为减小长度测量的误差,处理纸带时每五个点取一个计数点
C.必须选择打的第1个点与第2个点的间隔约为2mm
D.必须先接通电再释放纸带
(3)图2为实验中得到的一条纸带,O为打的第一个点,A、B、C、D、E为纸带十打点计时器打下的五个连续的点,测汁这五点到O点的距离分别为xA、xB、xC、xD、xE. 丁点计时器所接交流电的频率为f,当地的重力加速度为g,现用OC段验证机械能守恒定律,要验证的表达式为$g{x}_{c}=\frac{({x}_{D}-{x}_{E})^{2}{f}^{2}}{8}$,若实验中算得动能的增加量大于重力势能的减少量,可能原因是先释放纸带后接通电.
(4)根据打出的纸带算出离打第一个点较远处连续几个点时的速度,以$\frac{v^2}{2}$为纵轴,以x为横轴绘$\frac{v^2}{2}$-x图线,如果图线是过原点的斜的直线,且图线的斜率等于g,则机械能守恒得到验证;如果根据打点间隔算出打每个点重物运动的时间t,根据测得的x和算得的t,作出$\frac{x}{t}-t$图象,如果图线是过原点的斜的直线,且图线的斜率等于$\frac{g}{2}$,则机械能守恒定律得到验证.

分析 (1)由刻度尺来测量物体下落的高度.
(2)打点计时器要先工作再释放物体,顺序不能颠倒,而物体的质量不需要测量,对于间距及起点是否是从静止开始,没有严格的要求;
(3)根据物体下落,减小的重力势能转化为动能,那么由平均速度来求得瞬时速度,从而列出验证的表达式;当起点不是从静止开始运动,则增加的动能将会略大于减小的重力势能;
(4)由机械能守恒得:mgx=$\frac{1}{2}$mv2,所以$\frac{{v}^{2}}{2}$=gx,即图线是正比例函数图线,则斜率表示重力加速度;若作出$\frac{x}{t}-t$图象,根据运动学公式,即为平均速度与时间的图象,则图象的斜率表示重力加速度的一半.
解答 解:(1)实验中要测量重物下落的高度,必须用到测量工具刻度尺.
(2)由于只要验证$gh=\frac{{v}^{2}}{2}$即可,因此不需要测重物的质量,由于物体做落体运动时,打点的间隔较大,因此不需要每五个点取一个计数点,如果打的第1个点与第2个点的间隔不为2mm,可以取纸带中一段点迹清楚的部分,验证重物在打这两个点的时间间隔内机械能守恒即可,实验中必须先接通纸带再释放重物,D项正确.
(3)要验证的表达式为$mg{x}_{c}=\frac{1}{2}m{v}_{c}^{2}$
即$g{x}_{c}=\frac{1}{2}(\frac{{x}_{D}-{x}_{E}}{2}f)^{2}=\frac{({x}_{D}-{x}_{E})^{2}{f}^{2}}{8}$,
若实验中算得动能的增加量大于重力势能的减少量,可能原因是先释放纸带再接通电.
(4)如果机械能守恒,由$gh=\frac{{v}^{2}}{2}$可知,则$\frac{{v}^{2}}{2}-x$图线为一条过原点的斜的直线,图线的斜率为当地的重力加速度g;如果机械能守恒,则重物做自由落体运动,则$x=\frac{1}{2}g{t}^{2}$,$\frac{x}{t}$=$\frac{1}{2}gt$,因此$\frac{x}{t}-t$图线是一条过原点的直线,图线的斜率为当地重力加速度的一半,即$\frac{g}{2}$.
故答案为:(1)刻度尺;(2)D;
(3)$g{x}_{c}=\frac{({x}_{D}-{x}_{E})^{2}{f}^{2}}{8}$,先释放纸带后接通电;
(4)过原点的斜的直线,g; 过原点的斜的直线,$\frac{g}{2}$.
点评 本题考查了自由落体运动中机械能守恒的验证,用图象处理数据是非常重要的数学手段.同时注意第2问题:BC选项不一定是实验必须操作步骤,最后掌握平均速度与时间的图象斜率与重力加速度的关系,是解题的难点.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案 如图是“探究影响通电导体在磁场中受力因素”的实验示意图.三块相同马蹄形磁铁并列放置在水平桌面上,导体棒用图中1、2、3、4轻而柔软的细导线悬挂起来,它们之中的任意两根与导体棒和电源构成回路.认为导体棒所在位置附近为匀强磁场,最初导线1、4接在直流电源上,电源没有在图中画出.关于接通电源时可能出现的实验现象,下列叙述正确的是( )
如图是“探究影响通电导体在磁场中受力因素”的实验示意图.三块相同马蹄形磁铁并列放置在水平桌面上,导体棒用图中1、2、3、4轻而柔软的细导线悬挂起来,它们之中的任意两根与导体棒和电源构成回路.认为导体棒所在位置附近为匀强磁场,最初导线1、4接在直流电源上,电源没有在图中画出.关于接通电源时可能出现的实验现象,下列叙述正确的是( )| A. | 改变电流方向同时改变磁场方向,导体棒摆动方向将会改变 | |
| B. | 仅改变电流方向或者仅改变磁场方向,导体棒摆动方向一定改变 | |
| C. | 增大电流同时改变接入导体棒上的细导线,接通电源时,导体棒摆动幅度一定增大 | |
| D. | 仅拿掉中间的磁铁,导体棒摆动幅度不变 |
| A. | 地球上的物体均受到重力作用 | |
| B. | 同一物体在某处向上抛出后和向下抛出后所受重力不一样大 | |
| C. | 某物体在同一位置时,所受重力的大小与物体静止还是运动无关 | |
| D. | 物体所受重力大小与其质量有关 |

| A. | φA>φB>φC | B. | EA>EB>EC | C. | φA-φB=φB-φC | D. | EA=EB=EC |
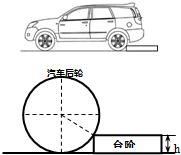 如图,某品牌汽车为后轮驱动,后轮直径为d,当汽车倒车遇到台阶时,两个后轮可同时缓慢倒上的台阶的最大高度为h,假设汽车轮胎和台阶的最大静摩擦力等于滑动摩擦力,且忽略轮胎的形变,不计前轮与地面的摩擦.则后轮与台阶的滑动摩擦系数为$\frac{2\sqrt{dh-{h}^{2}}}{d-2h}$;若该车缓慢倒上两个高度分别为h1和h2(h1<h2)的台阶,当后轮刚离开地面时,台阶对后轮的作用力分别为F1和F2,则F1大于F2.(选填“大于”、“小于”或“等于”)
如图,某品牌汽车为后轮驱动,后轮直径为d,当汽车倒车遇到台阶时,两个后轮可同时缓慢倒上的台阶的最大高度为h,假设汽车轮胎和台阶的最大静摩擦力等于滑动摩擦力,且忽略轮胎的形变,不计前轮与地面的摩擦.则后轮与台阶的滑动摩擦系数为$\frac{2\sqrt{dh-{h}^{2}}}{d-2h}$;若该车缓慢倒上两个高度分别为h1和h2(h1<h2)的台阶,当后轮刚离开地面时,台阶对后轮的作用力分别为F1和F2,则F1大于F2.(选填“大于”、“小于”或“等于”)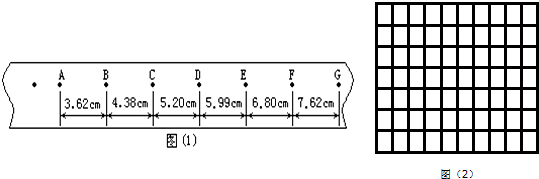
 如图所示,AB是倾角为θ的粗糙直轨道,BCD是光滑的圆弧轨道,AB恰好在B点与圆弧相切,圆弧的半径为R.一个质量为m的物体(可以看作质点)从直轨道上的P点由静止释放,结果它能在两轨道间做往返运动.已知P点与圆弧的圆心O等高,物体与轨道AB间的动摩擦因数为μ.求:
如图所示,AB是倾角为θ的粗糙直轨道,BCD是光滑的圆弧轨道,AB恰好在B点与圆弧相切,圆弧的半径为R.一个质量为m的物体(可以看作质点)从直轨道上的P点由静止释放,结果它能在两轨道间做往返运动.已知P点与圆弧的圆心O等高,物体与轨道AB间的动摩擦因数为μ.求: