题目内容
3. 从某一高度处水平抛出一物体,它着地时速度是50m/s,方向与水平方向成53°.取g=10m/s2,cos53°=0.6,sin53°=0.8,求:
从某一高度处水平抛出一物体,它着地时速度是50m/s,方向与水平方向成53°.取g=10m/s2,cos53°=0.6,sin53°=0.8,求:(1)抛出点的高度和水平射程.
(2)抛出后3s末的速度大小.
(3)抛出后3s内的位移大小.
分析 (1)根据速度关系求出落地时竖直方向的速度和水平方向速度,根据2gh=${{v}_{y}}^{2}$即可求得高度,根据t=$\frac{{v}_{y}}{g}$求解时间,根据x=v0t求解水平位移;
(2)根据vy=gt求解3s末竖直方向的速度,根据矢量合成原则求出3s末速度;
(3)求出3s内竖直方向位移,根据矢量合成原则求出3s内位移;
解答 解:(1)设初速度的大小为v0,根据题意,结合几何关系有:
v0=vcos53°=50×0.6m/s=30m/s,
竖直方向速度vy=vsin53°=50×0.8=40m/s,
运动时间t=$\frac{{v}_{y}}{g}=\frac{40}{10}=4s$
根据2gh=${{v}_{y}}^{2}$得:
下降的高度:h=$\frac{{{v}_{y}}^{2}}{2g}=\frac{1600}{20}=80m$,
水平位移x=v0t=30×4=120m
(2)3s末竖直方向的速度vy=gt=10×3=30m/s,则3s末的速度大小$v=\sqrt{3{0}^{2}+3{0}^{2}}=30\sqrt{2}m/s$
(3)3s内的水平位移x=v0t=30×3=90m,竖直方向位移h=$\frac{1}{2}g{t}^{2}=\frac{1}{2}×10×9=45m$,
则3s内的位移大小s=$\sqrt{{x}^{2}+{h}^{2}}=45\sqrt{5}m$
答:(1)抛出点的高度为80m,水平射程为120m.
(2)抛出后3s末的速度大小为$30\sqrt{2}m/s$.
(3)抛出后3s内的位移大小为$45\sqrt{5}m$
点评 本题就是对平抛运动规律的考查,平抛运动可以分解为在水平方向上的匀速直线运动,和竖直方向上的自由落体运动来求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
| A. | 重力、支持力 | B. | 重力、支持力、向心力和摩擦力 | ||
| C. | 重力、向心力 | D. | 重力、支持力和指向圆心的摩擦力 |
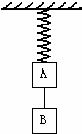 一根轻弹簧,下端系有质量为m的物体A,在A的下面再挂一个质量也是m的物体B,如图所示,在A、B保持静止时剪断AB间的细绳,如果A回到单独悬挂时的平衡位置的速率为v,而此时B的速率为u,那么在这段时间内弹力对A的冲量为( )
一根轻弹簧,下端系有质量为m的物体A,在A的下面再挂一个质量也是m的物体B,如图所示,在A、B保持静止时剪断AB间的细绳,如果A回到单独悬挂时的平衡位置的速率为v,而此时B的速率为u,那么在这段时间内弹力对A的冲量为( )| A. | m(v+u) | B. | m(v-u) | C. | mv | D. | mu |
| A. | 5m/s | B. | 1m/s | C. | 7m/s | D. | 0 |
 滑板运动是一项惊险刺激的运动,深受青少年的喜爱.图示是滑板运动的轨道,AB和CD是一段圆弧形轨道,BC是一段长l=7m的水平轨道.一运动员从AB轨道上的P点以vP=6m/s的速度下滑,经BC轨道后冲上CD轨道,到Q点时速度减为零.已知h=1.4m,H=1.8m,运动员的质量m=50kg,不计圆弧轨道上的摩擦,取g=10m/s2,求:
滑板运动是一项惊险刺激的运动,深受青少年的喜爱.图示是滑板运动的轨道,AB和CD是一段圆弧形轨道,BC是一段长l=7m的水平轨道.一运动员从AB轨道上的P点以vP=6m/s的速度下滑,经BC轨道后冲上CD轨道,到Q点时速度减为零.已知h=1.4m,H=1.8m,运动员的质量m=50kg,不计圆弧轨道上的摩擦,取g=10m/s2,求: 把一个用丝线悬挂的铅球放在电路中的线圈上方,如图所示,在下列三种情况下,悬挂铅球的丝线所受的拉力与铅球不在线圈上方时比较:
把一个用丝线悬挂的铅球放在电路中的线圈上方,如图所示,在下列三种情况下,悬挂铅球的丝线所受的拉力与铅球不在线圈上方时比较: