题目内容
15. 猴子通过树梢上的藤条越过河流的情景如图所示,图中BC是一条平坦的小路,长为4m,B端离河岸A处的水平距离为3m,AB两点恰好都在以O为圆心的圆周上.树梢上O点有一最大承受力为86N、长为5m、质量不计的藤条自然下垂,其末端刚好落在小路的左端B处.现有一只质量为5kg的猴子从平坦的小路C处由静止开始匀加速奔跑,到B处获得一定的水平速度并抓住藤条末端荡到河岸A处,不计猴子抓住藤条时的能量损失及空气阻力,重力加速度g=10m/s2.求猴子从B处安全荡到A处
猴子通过树梢上的藤条越过河流的情景如图所示,图中BC是一条平坦的小路,长为4m,B端离河岸A处的水平距离为3m,AB两点恰好都在以O为圆心的圆周上.树梢上O点有一最大承受力为86N、长为5m、质量不计的藤条自然下垂,其末端刚好落在小路的左端B处.现有一只质量为5kg的猴子从平坦的小路C处由静止开始匀加速奔跑,到B处获得一定的水平速度并抓住藤条末端荡到河岸A处,不计猴子抓住藤条时的能量损失及空气阻力,重力加速度g=10m/s2.求猴子从B处安全荡到A处(1)重力势能的改变量;
(2)在平坦小路B处的最小速度;
(3)在平坦小路上匀加速奔跑的加速度满足的条件.
分析 根据几何知识求出猴子下落的高度,进而求出重力势能的该变量;
猴子从B到A的过程中,减少的动能全部转化为重力势能时,速度最小,根据能量守恒求最小速度;
解答  解:(1)如图所示,过A点作OB的垂线,在直角三角形OAD中
解:(1)如图所示,过A点作OB的垂线,在直角三角形OAD中
xOD=$\sqrt{{{x}_{OA}}^{2}-{{x}_{AD}}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4m
△EP=mg(xOB-xOD)=50×(5-4)=50J
(2)猴子从B到A的过程中,减少的动能全部转化为重力势能时,速度最小.
$\frac{1}{2}$mv12=△EP
求得v1=2$\sqrt{5}$m/s
(3)猴子在平坦小路上加速,末速度为v1时,加速度最小.
a1=$\frac{{{v}_{1}}^{2}}{2{x}_{BC}}$=$\frac{(2\sqrt{5})^{2}}{2×4}$=2.5m/s2
猴子抓住藤条时,藤条刚好没有断开的条件,由牛顿第二定律得
T-mg=m$\frac{{{v}_{2}}^{2}}{{x}_{OB}}$
求得v2=6m/s
猴子在平坦小路上加速末速度为v2时,加速度最大.
a2=$\frac{{{v}_{2}}^{2}}{2{x}_{BC}}$=$\frac{{6}^{2}}{2×4}$=4.5m/s2
所以,猴子在平坦小路上加速度:2.5m/s2≤a≤4.5m/s2
答:(1)重力势能的改变量为50J;
(2)在平坦小路B处的最小速度为2$\sqrt{5}$m/s;
(3)在平坦小路上匀加速奔跑的加速度满足的条件2.5m/s2≤a≤4.5m/s2.
点评 本题要分析清楚物体的运动过程,根据物体的不同的运动状态,采用相应的物理规律求解即可.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3.如图所示,直导线M、N中通以方向相同的电流,则M对N的作用力的方向为( )


| A. | 垂直纸面向里 | B. | 垂直纸面向外 | C. | 垂直于N向上 | D. | 垂直于N向下 |
20.(1)某物理实验小组在使用多用电表按正确步骤测量某一电阻阻值,选择开关指在“×100”欧姆档,指针指示位置如图1所示,则这电阻阻值是2200Ω.
(2)然后他们用伏-安法来测未知电阻(电流表的内阻1Ω,电压表的内阻20kΩ);为了得到尽量多的数据、较精确测出电阻值,并要求电压从0开始调节,他们应选用图2中的B图所示电路进行实验.用此方法测出的电阻值比真实值偏大.(填“小”或“大”)
(3)在“用电流表和电压表测定电池的电动势和内阻”实验中,某同学测得了七组数据(如表).
①根据表中实验数据在图3中已描好点,试作出U-I图线;从图线中得出,电源电动势E=1.5V,内电阻r=1.18Ω.
②若一位同学未画出图线,只选用其中两组U和I的数据,根据公式E=U1+I1r和E=U2+I2r算出E和r,这样做可能得出误差很大的结果,则他选用其中第4组和第7组数据时算得的结果误差大.

(2)然后他们用伏-安法来测未知电阻(电流表的内阻1Ω,电压表的内阻20kΩ);为了得到尽量多的数据、较精确测出电阻值,并要求电压从0开始调节,他们应选用图2中的B图所示电路进行实验.用此方法测出的电阻值比真实值偏大.(填“小”或“大”)
(3)在“用电流表和电压表测定电池的电动势和内阻”实验中,某同学测得了七组数据(如表).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| U/v | 1.22 | 1.02 | 0.88 | 0.60 | 0.63 | 0.51 | 0.48 |
| I/A | 0.2 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 1.0 |
②若一位同学未画出图线,只选用其中两组U和I的数据,根据公式E=U1+I1r和E=U2+I2r算出E和r,这样做可能得出误差很大的结果,则他选用其中第4组和第7组数据时算得的结果误差大.

7.关于自由落体运动,下列说法中正确的是( )
| A. | 不考虑空气阻力的运动是自由落体运动 | |
| B. | 自由落体运动是初速度为零的匀加速运动 | |
| C. | 做自由落体运动的物体处于超重状态 | |
| D. | 做自由落体运动的物体,质量越大,下落得越快 |
4. 如图所示,绝缘细线上端固定,下端挂一轻质小球a,a的表面镀有铝膜;在a旁边固定有一绝缘金属球b,开始时a、b都不带电.使b带电时( )
如图所示,绝缘细线上端固定,下端挂一轻质小球a,a的表面镀有铝膜;在a旁边固定有一绝缘金属球b,开始时a、b都不带电.使b带电时( )
 如图所示,绝缘细线上端固定,下端挂一轻质小球a,a的表面镀有铝膜;在a旁边固定有一绝缘金属球b,开始时a、b都不带电.使b带电时( )
如图所示,绝缘细线上端固定,下端挂一轻质小球a,a的表面镀有铝膜;在a旁边固定有一绝缘金属球b,开始时a、b都不带电.使b带电时( )| A. | a不动 | B. | a远离b | ||
| C. | a靠近b | D. | a靠近b,并被b吸住不离开 |
5. 如图所示电路中,L为一自感系数较大的线圈,电键S闭合电路稳定后,在电阻R2和线圈L均有电流.现将电键S断开瞬间( )
如图所示电路中,L为一自感系数较大的线圈,电键S闭合电路稳定后,在电阻R2和线圈L均有电流.现将电键S断开瞬间( )
 如图所示电路中,L为一自感系数较大的线圈,电键S闭合电路稳定后,在电阻R2和线圈L均有电流.现将电键S断开瞬间( )
如图所示电路中,L为一自感系数较大的线圈,电键S闭合电路稳定后,在电阻R2和线圈L均有电流.现将电键S断开瞬间( )| A. | 流经R2和L的电流方向都向左 | |
| B. | 流经R2和L的电流方向都向右 | |
| C. | 流经R2的电流方向向右,流经L的电流方向向左 | |
| D. | 流经R2的电流方向向左,流经L的电流方向向右 |
 如图所示,长为l的细绳的一端系一小球,另一端悬于距光滑的平面上方h高处(h<l).当球在水平上以转速n做匀速圆周运动时,水平面受到的压力为多大?为使小球不离开平面,n的最大值是多少?
如图所示,长为l的细绳的一端系一小球,另一端悬于距光滑的平面上方h高处(h<l).当球在水平上以转速n做匀速圆周运动时,水平面受到的压力为多大?为使小球不离开平面,n的最大值是多少? 如图所示,半径为R=0.4m的$\frac{1}{4}$光滑圆弧轨道AB与粗糙的水平轨道BO相切于B点,一带电量q=+0.2C质量m=0.4kg的小物块从A点由静止释放,经过BO后以v=1m/s的速度从O点水平抛出,击中右下侧挡板上的P点.以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板形状满足方程y=x2-6(x和y的单位均为m),在y轴的左侧区域存在竖直向下的匀强电场,场强E=20V/m,小物块与轨道BO间的动摩擦因数μ=0.1,g 取10m/s2.求
如图所示,半径为R=0.4m的$\frac{1}{4}$光滑圆弧轨道AB与粗糙的水平轨道BO相切于B点,一带电量q=+0.2C质量m=0.4kg的小物块从A点由静止释放,经过BO后以v=1m/s的速度从O点水平抛出,击中右下侧挡板上的P点.以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板形状满足方程y=x2-6(x和y的单位均为m),在y轴的左侧区域存在竖直向下的匀强电场,场强E=20V/m,小物块与轨道BO间的动摩擦因数μ=0.1,g 取10m/s2.求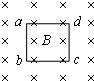 如图所示,穿过单匝闭合线圈abcd的磁通量在0.2s内由0.4Wb均匀增大到0.8Wb,则在此过程中穿过该线圈的磁通量的变化量为0.4Wb,该线圈中产生的感应电动势为2V.
如图所示,穿过单匝闭合线圈abcd的磁通量在0.2s内由0.4Wb均匀增大到0.8Wb,则在此过程中穿过该线圈的磁通量的变化量为0.4Wb,该线圈中产生的感应电动势为2V.