题目内容
6.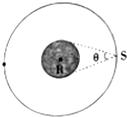 如图所示,某卫星S绕地球做周期为T的匀速圆周运动,地球相对于卫星S的张角为θ.地球视为质量分布均匀的球体,其表面重力加速度为g,引力常量为G.求:
如图所示,某卫星S绕地球做周期为T的匀速圆周运动,地球相对于卫星S的张角为θ.地球视为质量分布均匀的球体,其表面重力加速度为g,引力常量为G.求:(1)卫星S的速度大小;
(2)地球的第一宇宙速度.
分析 根据几何关系求得卫星轨道半径,根据万有引力提供圆周运动向心力和万有引力等于重力求解.
解答 解:(1)由题意令卫星的轨道半径为r,地球的半径为R,根据几何关系可知,
r=$\frac{R}{sin\frac{θ}{2}}$
根据万有引力提供向心力得:$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r
T=2π $\sqrt{\frac{{r}^{3}}{GM}}$
根据万有引力等于重力,有:$\frac{GMm}{{R}^{2}}$=mg,
联立解得:R=$\frac{{{gT}^{2}si{n}^{3}(\frac{θ}{2})}^{\;}}{{4π}^{2}}$,r=$\frac{{{gT}^{2}si{n}^{2}(\frac{θ}{2})}^{\;}}{{4π}^{2}}$
卫星S的速度大小为:v=$\frac{2πr}{T}$=$\frac{Tg}{2π}$sin2$\frac{θ}{2}$,
(2)根据万有引力提供向心力得:
mg=m$\frac{{v}^{2}}{R}$
v=$\sqrt{gR}$=$\frac{Tg}{2π}$$\sqrt{{sin}^{3}\frac{θ}{2}}$,
答:(1)卫星S的速度大小是$\frac{Tg}{2π}$sin2$\frac{θ}{2}$;
(2)地球的第一宇宙速度是$\frac{Tg}{2π}$$\sqrt{{sin}^{3}\frac{θ}{2}}$.
点评 解决本题的关键是能根据几何关系求得卫星轨道半径与地球半径的大小关系,这是学生容易出错的主要地方.

练习册系列答案
相关题目
17.一个物体做曲线运动,则这个物体( )
| A. | 一定是做加速度不变的运动 | |
| B. | 一定是做加速度变化的运动 | |
| C. | 做速度大小不断变化但速度方向可能不变的运动 | |
| D. | 做速度方向不断变化但速度大小可能不变的运动 |
14. 如图所示,有一个半径为R的光滑圆形圆管轨道(忽略圆管内径),一小球处于圆管内,现给小球有一个初速度,使小球在竖直面内做圆周运动,小球过最高点的速度为v,下列叙述正确的是( )
如图所示,有一个半径为R的光滑圆形圆管轨道(忽略圆管内径),一小球处于圆管内,现给小球有一个初速度,使小球在竖直面内做圆周运动,小球过最高点的速度为v,下列叙述正确的是( )
 如图所示,有一个半径为R的光滑圆形圆管轨道(忽略圆管内径),一小球处于圆管内,现给小球有一个初速度,使小球在竖直面内做圆周运动,小球过最高点的速度为v,下列叙述正确的是( )
如图所示,有一个半径为R的光滑圆形圆管轨道(忽略圆管内径),一小球处于圆管内,现给小球有一个初速度,使小球在竖直面内做圆周运动,小球过最高点的速度为v,下列叙述正确的是( )| A. | 小球过最低点的最小速度为2$\sqrt{gR}$ | |
| B. | v增大,轨道对球的弹力也增大 | |
| C. | 当v由$\sqrt{gR}$值逐渐减小时,轨道对小球的弹力也逐渐减小 | |
| D. | 当v由$\sqrt{gR}$值逐渐增大时,轨道对小球的弹力也逐渐增大 |
1. 如图所示,在一次中学生物理竞赛中,赛题是从桌角A处向B处发射一个乒乓球,让竞赛者在桌边的B处用一支吹管将球吹进球门C,要使射门可能成功,参赛者吹气方向应为( )
如图所示,在一次中学生物理竞赛中,赛题是从桌角A处向B处发射一个乒乓球,让竞赛者在桌边的B处用一支吹管将球吹进球门C,要使射门可能成功,参赛者吹气方向应为( )
 如图所示,在一次中学生物理竞赛中,赛题是从桌角A处向B处发射一个乒乓球,让竞赛者在桌边的B处用一支吹管将球吹进球门C,要使射门可能成功,参赛者吹气方向应为( )
如图所示,在一次中学生物理竞赛中,赛题是从桌角A处向B处发射一个乒乓球,让竞赛者在桌边的B处用一支吹管将球吹进球门C,要使射门可能成功,参赛者吹气方向应为( )| A. | 水平向左吹 | B. | 对准C吹 | C. | 向左下方吹 | D. | 向右下方吹 |
11.一正弦交流电的电压随时间变化的规律如图所示.由图可知( )


| A. | 该交流电的电压瞬时值的表达式为μ=100sin(25πt)V | |
| B. | 该交流电的频率为50Hz | |
| C. | 该交流电的电压的有效值为100$\sqrt{2}$ | |
| D. | 若将该交流电压加在阻值R=100Ω的电阻两端,则电阻消耗的功率是50W |
6. 我国自主研制的四代战机歼31在第十届中国国际航空航天博览会上实机表演,起飞后首先进行大角度爬升,运动轨迹如图所示.若爬升过程速度大小保持不变,则这段时间战机在水平方向的分运动是( )
我国自主研制的四代战机歼31在第十届中国国际航空航天博览会上实机表演,起飞后首先进行大角度爬升,运动轨迹如图所示.若爬升过程速度大小保持不变,则这段时间战机在水平方向的分运动是( )
 我国自主研制的四代战机歼31在第十届中国国际航空航天博览会上实机表演,起飞后首先进行大角度爬升,运动轨迹如图所示.若爬升过程速度大小保持不变,则这段时间战机在水平方向的分运动是( )
我国自主研制的四代战机歼31在第十届中国国际航空航天博览会上实机表演,起飞后首先进行大角度爬升,运动轨迹如图所示.若爬升过程速度大小保持不变,则这段时间战机在水平方向的分运动是( )| A. | 匀速直线运动 | B. | 加速直线运动 | ||
| C. | 减速直线运动 | D. | 先加速后减速运动 |
 质量为30kg的小孩坐在10kg的雪橇上,大人用与水平方向成37°斜向上的拉力拉雪橇,力的大小为100N,雪橇与地面间的动摩擦因数为0.2,求:
质量为30kg的小孩坐在10kg的雪橇上,大人用与水平方向成37°斜向上的拉力拉雪橇,力的大小为100N,雪橇与地面间的动摩擦因数为0.2,求: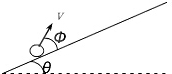 如图所示,倾角为θ的斜面光滑,自斜面上某处以速度v与斜面夹角为Φ的方向向斜面上抛出一质点(设质点与斜面间的碰撞是完全弹性的,即球入射方向与反射遵循光的反射定律),斜面足够长,要求质点最后仍能回到原出发点.问:Φ角应满足什么条件?
如图所示,倾角为θ的斜面光滑,自斜面上某处以速度v与斜面夹角为Φ的方向向斜面上抛出一质点(设质点与斜面间的碰撞是完全弹性的,即球入射方向与反射遵循光的反射定律),斜面足够长,要求质点最后仍能回到原出发点.问:Φ角应满足什么条件? 某兴趣小组对一辆自制遥控小车的性能进行研究,他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2s~10s时间段图象为曲线外,其余时间段图象均为直线).已知在小车运动的过程中,2s~14s时间段内小车的功率保持不变,在14s末停止遥控而让小车自由滑行,小车的质量为1.0kg,可认为在整个运动过程中小车所受到的阻力大小不变.求:
某兴趣小组对一辆自制遥控小车的性能进行研究,他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2s~10s时间段图象为曲线外,其余时间段图象均为直线).已知在小车运动的过程中,2s~14s时间段内小车的功率保持不变,在14s末停止遥控而让小车自由滑行,小车的质量为1.0kg,可认为在整个运动过程中小车所受到的阻力大小不变.求: