题目内容
18. 用如图所示的装置可验证机械能守恒定律,直径为d的摆球A拴在长为L的不可伸长的轻绳一端(L>>d),绳的另一端固定在O点,O点正下方摆球重心经过的位置固定光电门B.现将摆球拉起,使绳偏离竖直方向θ角时,由静止开始释放摆球,当其通过最低位置时,光电门B记录的遮光时间为t.
用如图所示的装置可验证机械能守恒定律,直径为d的摆球A拴在长为L的不可伸长的轻绳一端(L>>d),绳的另一端固定在O点,O点正下方摆球重心经过的位置固定光电门B.现将摆球拉起,使绳偏离竖直方向θ角时,由静止开始释放摆球,当其通过最低位置时,光电门B记录的遮光时间为t.(1)摆球通过最低点的速度v=$\frac{d}{t}$(用题中字母表示)
(2)写出满足机械能守恒的表达式$\frac{1}{2}$($\frac{d}{t}$)2=gL(1-cosθ)(用题中字母表示)
分析 (1)最低点的速度采用平均速度来等效替代瞬时速度;
(2)根据机械能守恒的表达式列式即可求得机械能的表达式.
解答 解:(1)在最低点时,通过的距离为d,小球经过的时间为t,则平均速度v=$\frac{d}{t}$;
(3)由机械能守恒定律可知,mgh=$\frac{1}{2}$mv2;
h=L(1-cosθ)
则有:$\frac{1}{2}$m($\frac{d}{t}$)2=mgL(1-cosθ)
因此机械能守恒表达式为:$\frac{1}{2}$($\frac{d}{t}$)2=gL(1-cosθ)
故答案为:(1)$\frac{d}{t}$
(2)$\frac{1}{2}$($\frac{d}{t}$)2=gL(1-cosθ)
点评 本题考查机械能守恒定律的实验内容;要求学生能掌握正确的求解思路,并能根据平均速度与瞬时速度的关系表示瞬时速度.

练习册系列答案
相关题目
8.甲、乙两物体从同一时刻出发沿同一直线运动的x-t图象如图所示,下列判断正确的是( )


| A. | 甲做匀速直线运动,乙做匀变速直线运动 | |
| B. | 乙在前2s内做匀加速直线运动,2s后做匀减速直线运动 | |
| C. | 两物体两次分别在1s末和4s末到达同一位置 | |
| D. | 0~6s内,乙的位移比甲大 |
9.某同学将原来静止在地面上的质量为1kg的物体竖直向上提高1m,并使物体获得2m/s的速度,取g=10m/s2.在此过程中( )
| A. | 物体重力势能增加10J | B. | 合外力对物体做功12J | ||
| C. | 人对物体做功2J | D. | 物体机械能增加12J |
6. 如图甲所示某汽车以不变的速率驶入一个狭长的水平90°圆弧形弯道,弯道两端连接的都是直道,有人在车内测量汽车的向心加速度随时间的变化关系如图乙所示,则变道的半径为( )
如图甲所示某汽车以不变的速率驶入一个狭长的水平90°圆弧形弯道,弯道两端连接的都是直道,有人在车内测量汽车的向心加速度随时间的变化关系如图乙所示,则变道的半径为( )
 如图甲所示某汽车以不变的速率驶入一个狭长的水平90°圆弧形弯道,弯道两端连接的都是直道,有人在车内测量汽车的向心加速度随时间的变化关系如图乙所示,则变道的半径为( )
如图甲所示某汽车以不变的速率驶入一个狭长的水平90°圆弧形弯道,弯道两端连接的都是直道,有人在车内测量汽车的向心加速度随时间的变化关系如图乙所示,则变道的半径为( )| A. | 12.5m | B. | 50m | C. | 200m | D. | 100m |
3. 如图所示,在光滑的水平地面上,水平恒力拉动小车和木块做加速运动,小车的质量为M,木块的质量为m,它们的共同加速度为a,木块与小车间的动摩擦因数为μ.则在运动过程中( )
如图所示,在光滑的水平地面上,水平恒力拉动小车和木块做加速运动,小车的质量为M,木块的质量为m,它们的共同加速度为a,木块与小车间的动摩擦因数为μ.则在运动过程中( )
 如图所示,在光滑的水平地面上,水平恒力拉动小车和木块做加速运动,小车的质量为M,木块的质量为m,它们的共同加速度为a,木块与小车间的动摩擦因数为μ.则在运动过程中( )
如图所示,在光滑的水平地面上,水平恒力拉动小车和木块做加速运动,小车的质量为M,木块的质量为m,它们的共同加速度为a,木块与小车间的动摩擦因数为μ.则在运动过程中( )| A. | 木块受到的摩擦力为μmg | B. | 木块受到的摩擦力为ma | ||
| C. | 小车受到的摩擦力为$\frac{Fm}{m+M}$ | D. | 小车受到的合力为$\frac{FM}{m+M}$ |
7.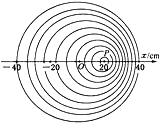 如图所示,让小球P一边贴水面每秒振动5次,一边沿x轴正方向匀速移动,O点是它的初始位置.图示为观察到的某一时刻的水面波,图中的实线表示水面波的波峰位置.那么此水面波的传播速度及小球P匀速移动的速度分别是( )
如图所示,让小球P一边贴水面每秒振动5次,一边沿x轴正方向匀速移动,O点是它的初始位置.图示为观察到的某一时刻的水面波,图中的实线表示水面波的波峰位置.那么此水面波的传播速度及小球P匀速移动的速度分别是( )
 如图所示,让小球P一边贴水面每秒振动5次,一边沿x轴正方向匀速移动,O点是它的初始位置.图示为观察到的某一时刻的水面波,图中的实线表示水面波的波峰位置.那么此水面波的传播速度及小球P匀速移动的速度分别是( )
如图所示,让小球P一边贴水面每秒振动5次,一边沿x轴正方向匀速移动,O点是它的初始位置.图示为观察到的某一时刻的水面波,图中的实线表示水面波的波峰位置.那么此水面波的传播速度及小球P匀速移动的速度分别是( )| A. | 0.05m/s、0.025m/s | B. | 0.1m/s、0.05m/s | ||
| C. | 0.15m/s、0.125m/s | D. | 0.2m/s、0.1m/s |
8.在沙漠中旅游时,最刺激的莫过于滑沙运动.某人坐在滑沙板上从沙坡斜面的顶端由静止沿直线下滑到斜面底端时,速度为2v0,设人下滑时所受阻力恒定不变,沙坡长度为L,斜面倾角为α,人的质量为m,滑沙板质量不计,重力加速度为g.则( )
| A. | 人沿沙坡下滑时所受阻力Ff大小为mgsinα+$\frac{2m{{v}_{0}}^{2}}{L}$ | |
| B. | 人在下滑过程中重力功率的最大值为2mgv0sinα | |
| C. | 若人在斜面顶端被其他人推了一把,沿斜面以v0的初速度下滑,则人到达斜面低端时的速度大小为3v0 | |
| D. | 若人在斜面顶端被其他人推了一把,沿斜面以v0的初速度下滑,则人到达斜面低端时的速度大小为$\sqrt{5}$v0 |
 在某次光电效应实验中,得到的遏制电压u0与入射光的频率v的关系如图所示,若该直线的斜率为k、横截距为b,电子电荷量的绝对值为e,则普朗克常量可表示为ek,所用材料的逸出功可表示为keb.
在某次光电效应实验中,得到的遏制电压u0与入射光的频率v的关系如图所示,若该直线的斜率为k、横截距为b,电子电荷量的绝对值为e,则普朗克常量可表示为ek,所用材料的逸出功可表示为keb.