题目内容
长为L的细线一端固定于O点,如图所示,另一端拴一质量为m的小球.把小球拉至最高点A,以水平速度v抛出.求当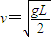 时,球运动到最低点C时细线的拉力大小.
时,球运动到最低点C时细线的拉力大小.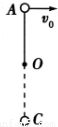
【答案】分析:由小球受重力与向心力的关系可得出小球的运动状态为圆周运动还是平抛运动;再根据机械能守恒可求得最低点时的速度,由牛顿第二定律可求得绳子的拉力.
解答:解:由于v=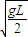 ,小于小球做圆周运动通过最高点时的最小速度
,小于小球做圆周运动通过最高点时的最小速度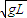 ,故小球做平抛运动,设小球运动到如图所示的B点时细线绷紧,此时细线与竖直方向的夹角为θ,由平抛运动规律有:Lsinθ=vt;
,故小球做平抛运动,设小球运动到如图所示的B点时细线绷紧,此时细线与竖直方向的夹角为θ,由平抛运动规律有:Lsinθ=vt;
L(1-cosθ)= gt2
gt2
解得:θ=90°,说明B与O在同一直线上,vBx=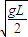 ,由于细线瞬时绷紧,使小球水平速度突然变为零,所以此绷紧过程有机械能损失,然后小球以
,由于细线瞬时绷紧,使小球水平速度突然变为零,所以此绷紧过程有机械能损失,然后小球以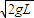 的速度从B点开始做圆周运动到C点,由机械能守恒有:
的速度从B点开始做圆周运动到C点,由机械能守恒有:
 mvBy2+mgL=
mvBy2+mgL= mvC2
mvC2
在最低点C有:T-mg=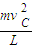
解得小球在最低点C时绳的拉力T=5mg.
点评:本题结合平抛运动及圆周运动进行考查,注意绳在绷紧过程中会发生突变,造成能量损失.
解答:解:由于v=
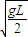 ,小于小球做圆周运动通过最高点时的最小速度
,小于小球做圆周运动通过最高点时的最小速度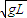 ,故小球做平抛运动,设小球运动到如图所示的B点时细线绷紧,此时细线与竖直方向的夹角为θ,由平抛运动规律有:Lsinθ=vt;
,故小球做平抛运动,设小球运动到如图所示的B点时细线绷紧,此时细线与竖直方向的夹角为θ,由平抛运动规律有:Lsinθ=vt;L(1-cosθ)=
 gt2
gt2解得:θ=90°,说明B与O在同一直线上,vBx=
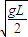 ,由于细线瞬时绷紧,使小球水平速度突然变为零,所以此绷紧过程有机械能损失,然后小球以
,由于细线瞬时绷紧,使小球水平速度突然变为零,所以此绷紧过程有机械能损失,然后小球以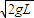 的速度从B点开始做圆周运动到C点,由机械能守恒有:
的速度从B点开始做圆周运动到C点,由机械能守恒有: mvBy2+mgL=
mvBy2+mgL= mvC2
mvC2在最低点C有:T-mg=
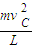
解得小球在最低点C时绳的拉力T=5mg.
点评:本题结合平抛运动及圆周运动进行考查,注意绳在绷紧过程中会发生突变,造成能量损失.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 一条长为L的细线一端固定在O点,另一端系着质量为m,带电量为-q的小球,整个装置处于足够大的水平方向的匀强电场中,静止于A点,此时细线与竖直方向成45°角,如图所示,现将小球沿圆周移动到O点的正止方B点,然后由静止释放.
一条长为L的细线一端固定在O点,另一端系着质量为m,带电量为-q的小球,整个装置处于足够大的水平方向的匀强电场中,静止于A点,此时细线与竖直方向成45°角,如图所示,现将小球沿圆周移动到O点的正止方B点,然后由静止释放. (附加题) 长为L的细线一端固定一个带正电小球,另一端固定在O点,且处在一匀强电场中,小球受到的电场力等于其重力的
(附加题) 长为L的细线一端固定一个带正电小球,另一端固定在O点,且处在一匀强电场中,小球受到的电场力等于其重力的
 ,小球才能通过A点
,小球才能通过A点
 倍.当电场的取向合适时,可使小球在与水平方向成30°角的倾斜平面内做圆周运动,求此圆周运动的最大速度以及此时电场的方向.
倍.当电场的取向合适时,可使小球在与水平方向成30°角的倾斜平面内做圆周运动,求此圆周运动的最大速度以及此时电场的方向.