题目内容
17.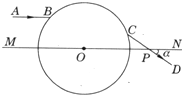 如图所示,一透明球体置于空气中,球半径为R=10Cm,折射率n=$\sqrt{2}$.MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,其中B为入射点,AB与MN间距为5$\sqrt{2}$cm,CD为出射光线.
如图所示,一透明球体置于空气中,球半径为R=10Cm,折射率n=$\sqrt{2}$.MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,其中B为入射点,AB与MN间距为5$\sqrt{2}$cm,CD为出射光线.①补全折射光路图并求出光从B点传到C点的时间;
②求CD与MN所成的角a.
分析 ①连接BC,作出光路图.由几何知识求出光线在B点时的入射角,根据折射定律求出折射角,由几何关系求出BC,由n=$\frac{c}{v}$求出光在球体中传播的速度v,再求解光从B点传到C点的时间;
②根据几何知识求出CD与MN所成的角α.
解答  解:(1)画出光路图如图.
解:(1)画出光路图如图.
由几何知识有:sini=$\frac{BE}{BO}$=$\frac{5\sqrt{2}}{10}$=$\frac{\sqrt{2}}{2}$,得 i=45°
由n=$\frac{sini}{sinr}$=$\sqrt{2}$
解得:r=30°
由几何关系可得B到C的距离为:s=2Rcos30°=$\sqrt{3}$R
光在球体中传播速度为:v=$\frac{c}{n}$
故光从B点传到C点的时间为:t=$\frac{s}{v}$=$\frac{\sqrt{3}R}{\frac{c}{n}}$=$\frac{\sqrt{3}nR}{c}$=$\frac{\sqrt{3}×\sqrt{2}×0.1}{3×1{0}^{8}}$s=$\frac{\sqrt{6}}{3}$×10-9s
(2)根据光路可逆原理得知光线射出球体时的折射角等于i=45°
由几何关系得:∠BOC=120°,∠BOE=45°,∠COP=180°-∠BOC-∠BOE=15°
故α=i-∠COP=45°-15°=30°
答:(1)光从B点传到C点的时间是$\frac{\sqrt{6}}{3}$×10-9s.
(2)CD与MN所成的角α是30°.
点评 本题是几何光学问题,作出光路图是解题的基础,此类问题往往是折射定律、光速公式和几何知识的综合应用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
7. 如图所示,在同一水平面上有A、B、C、D四个点,其上分别放上带电荷量分别为-q、Q、-q、Q的点电荷.四个点电荷构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )
如图所示,在同一水平面上有A、B、C、D四个点,其上分别放上带电荷量分别为-q、Q、-q、Q的点电荷.四个点电荷构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )
 如图所示,在同一水平面上有A、B、C、D四个点,其上分别放上带电荷量分别为-q、Q、-q、Q的点电荷.四个点电荷构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )
如图所示,在同一水平面上有A、B、C、D四个点,其上分别放上带电荷量分别为-q、Q、-q、Q的点电荷.四个点电荷构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )| A. | cos3 α=$\frac{q}{8Q}$ | B. | cos3 α=$\frac{{q}^{2}}{{Q}^{2}}$ | C. | sin3 α=$\frac{Q}{8q}$ | D. | sin3 α=$\frac{{Q}^{2}}{{q}^{2}}$ |
8.2013年10月11日,在天津举行的第六届东亚运动会女子4×200米自由泳接力赛中,中国队以8分06秒06的成绩夺得冠军.中国队之所以能够取得这个项目的冠军,取决于她们在这800米中( )
| A. | 平均速率大 | B. | 平均速度大 | ||
| C. | 冲刺时的瞬时速度大 | D. | 某一时刻的瞬时速度大 |
5.在一次抗洪抢险中,抢险队员驾驶冲锋舟准备度过某河.已知该河宽80m,河中各点的河水速度大小与该点到河岸的距离成正比,冲锋舟在静水中的速度恒为4m/s,且渡河过程中,河水速度大小将随上游降雨量的变化而变化.关于上述渡河过程,下列说法正确的是( )
| A. | 抢险队员到达对岸的最短时间是20s,这一时间与河水速度大小是否变化无关 | |
| B. | 随着河水速度大小的变化,船到达对岸的最短时间会相应变化 | |
| C. | 若冲锋舟的船头始终垂直于河岸,当它距离岸40m处的河水速度大小是3m/s,则此时船的实际速度是5m/s | |
| D. | 无论河水速度多大,也无论抢险队员怎样调整船的航向,冲锋舟都无法到达河对岸 |
2.下面关于力的说法正确的是( )
| A. | 两个物体相互接触一定会产生弹力 | |
| B. | 用一根线竖直悬挂的物体静止时,线拉力方向所在的直线一定通过物体的重心 | |
| C. | 舞蹈演员在做各种优美的动作时,其重心在体内位置不变 | |
| D. | 弹力的大小与物体的形变程度有关,形变程度越大,弹力越大 |
9.质量m=2kg的物体从距离地面高5m处以v0=2m/s的速度水平抛出,g取10m/s2,则物体落地时的水平位移为( )
| A. | 2m | B. | 5m | C. | 10m | D. | 20m |
6.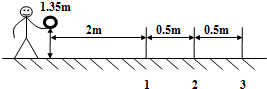 “套圈”是一项老少皆宜的体育运动项目.如图所示,水平地面上固定着3根直杆1、2、3,直杆的粗细不计,高度均为0.1m,相邻两直杆之间的距离为0.5m.比赛时,运动员将内圆直径为0.2m的环沿水平方向抛出,刚抛出时环平面距地面的高度为1.35m,环的中心与直杆1的水平距离为2m.假设直杆与环的中心位于同一竖直面,且运动中环心始终在该平面上,环面在空中保持水平,忽略空气阻力的影响,g取10m/s2.以下说法正确的是( )
“套圈”是一项老少皆宜的体育运动项目.如图所示,水平地面上固定着3根直杆1、2、3,直杆的粗细不计,高度均为0.1m,相邻两直杆之间的距离为0.5m.比赛时,运动员将内圆直径为0.2m的环沿水平方向抛出,刚抛出时环平面距地面的高度为1.35m,环的中心与直杆1的水平距离为2m.假设直杆与环的中心位于同一竖直面,且运动中环心始终在该平面上,环面在空中保持水平,忽略空气阻力的影响,g取10m/s2.以下说法正确的是( )
 “套圈”是一项老少皆宜的体育运动项目.如图所示,水平地面上固定着3根直杆1、2、3,直杆的粗细不计,高度均为0.1m,相邻两直杆之间的距离为0.5m.比赛时,运动员将内圆直径为0.2m的环沿水平方向抛出,刚抛出时环平面距地面的高度为1.35m,环的中心与直杆1的水平距离为2m.假设直杆与环的中心位于同一竖直面,且运动中环心始终在该平面上,环面在空中保持水平,忽略空气阻力的影响,g取10m/s2.以下说法正确的是( )
“套圈”是一项老少皆宜的体育运动项目.如图所示,水平地面上固定着3根直杆1、2、3,直杆的粗细不计,高度均为0.1m,相邻两直杆之间的距离为0.5m.比赛时,运动员将内圆直径为0.2m的环沿水平方向抛出,刚抛出时环平面距地面的高度为1.35m,环的中心与直杆1的水平距离为2m.假设直杆与环的中心位于同一竖直面,且运动中环心始终在该平面上,环面在空中保持水平,忽略空气阻力的影响,g取10m/s2.以下说法正确的是( )| A. | 如果能够套中直杆,环抛出时的水平初速度不能小于3.9m/s | |
| B. | 如果能够套中第2根直杆,环抛出时的水平初速度范围在4.8m/s到5.2m/s之间 | |
| C. | 如环抛出的水平速度大于6.1m/s,就不能套中第3根直杆 | |
| D. | 如以4m/s的水平初速度将环抛出,就可以套中第1根直杆 |
1. 如图所示,一辆小车静止在水平地面上,车内固定着一个倾角为60°的光滑斜面OA,光滑挡板OB可绕转轴O在竖直平面内转动.现将一重力为G的圆球放在斜面与挡板之间,挡板与水平面的夹角θ=60°.下列说法正确的是( )
如图所示,一辆小车静止在水平地面上,车内固定着一个倾角为60°的光滑斜面OA,光滑挡板OB可绕转轴O在竖直平面内转动.现将一重力为G的圆球放在斜面与挡板之间,挡板与水平面的夹角θ=60°.下列说法正确的是( )
 如图所示,一辆小车静止在水平地面上,车内固定着一个倾角为60°的光滑斜面OA,光滑挡板OB可绕转轴O在竖直平面内转动.现将一重力为G的圆球放在斜面与挡板之间,挡板与水平面的夹角θ=60°.下列说法正确的是( )
如图所示,一辆小车静止在水平地面上,车内固定着一个倾角为60°的光滑斜面OA,光滑挡板OB可绕转轴O在竖直平面内转动.现将一重力为G的圆球放在斜面与挡板之间,挡板与水平面的夹角θ=60°.下列说法正确的是( )| A. | 若保持挡板不动,则球对斜面的压力大小为G | |
| B. | 若挡板从图示位置顺时针方向缓慢转动60°,则球对斜面的压力逐渐增大 | |
| C. | 若挡板从图示位置顺时针方向缓慢转动60°,则球对挡板的压力逐渐减小 | |
| D. | 若保持挡板不动,使小车水平向右做匀加速直线运动,则球对挡板的压力不可能为零 |