题目内容
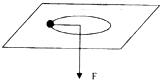如图所示，一个被绳子牵引的小球在光滑水平板上以速度v=1.0m/s做匀速圆周运动．运动半径r=30cm．现迅速松手使绳子放长20cm后立即拽紧绳子，使小球在更大半径的新轨道上做匀速圆周运动．求：（1）实现这一过渡所需要的时间．
（2）小球在新轨道上做匀速圆周运动时，绳子对小球的牵引力F2是原来绳子对小球的牵引力F1的多少倍？
分析：（1）结合几何关系求出过渡时的位移，从而根据匀速直线运动的位移公式求出过渡所需的时间．
（2）根据平行四边形定则求出绳子拉紧后瞬间的速度，根据拉力提供向心力，求出两次拉力的大小，从而得出拉力的关系．
（2）根据平行四边形定则求出绳子拉紧后瞬间的速度，根据拉力提供向心力，求出两次拉力的大小，从而得出拉力的关系．
解答：解：（1）松手后小球沿速度方向做匀速直线运动，
OB=50cm，AB=40cm
则t=
=
s=0.4s．
（2）绳子被拉紧瞬间速度变为v1
v1=vsin37°=0.6m/s
则F1=m
，F2=m
则
=
=
=
绳子对小球的牵引力F2是原来绳子对小球的牵引力F1的
．
答：（1）实现这一过渡所需要的时间为0.4s．
（2）绳子对小球的牵引力F2是原来绳子对小球的牵引力F1的
．
OB=50cm，AB=40cm
则t=
| AB |
| v |
| 0.4 |
| 1 |
（2）绳子被拉紧瞬间速度变为v1
v1=vsin37°=0.6m/s
则F1=m
| v2 |
| r |
| v12 |
| OB |
则
| F1 |
| F2 |
| v2?OB |
| v12?r |
| 1×0.5 |
| 0.36×0.3 |
| 125 |
| 27 |
绳子对小球的牵引力F2是原来绳子对小球的牵引力F1的
| 27 |
| 125 |
答：（1）实现这一过渡所需要的时间为0.4s．
（2）绳子对小球的牵引力F2是原来绳子对小球的牵引力F1的
| 27 |
| 125 |
点评：解决本题的关键知道绳子拉紧的瞬间，沿绳子方向的速度减为零，从而得出两次圆周运动速度的大小关系．
练习册系列答案
阅读快车系列答案
相关题目
用两根能承受的最大拉力相等，长度不等的细绳AO、BO，如图所示悬挂一个中空铁球，当在球内不断注入铁砂时，若绳子终将被拉断，则（ ）
如图所示，一个重10N的光滑重球被一根细绳挂在竖直墙壁上的A点，绳子和墙壁的夹角θ为37°，取cos37°=0.8，sin37°=0.6．求：
如图所示，一个半径为r、重为G的圆球，被长为r的细绳挂在竖直的光滑的墙壁上，绳与墙所成的角度为30°，则绳子的拉力T和墙壁的弹力N分别是（ ）
（2009?中山市模拟）如图所示，一个质量为m的小球由两根细绳拴在竖直转轴上的A、B两处，AB间距为L，A处绳长为