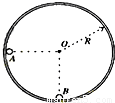
题目内容
如图,半径为R的光滑圆形轨道固定在竖直面内.小球A、B质量分别为m、βm(β为待定系数).A球从左边与圆心等高处由静止开始沿轨道下滑,与静止于轨道最低点的B球相撞,碰撞后A、B球能达到的最大高度均为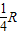 ,碰撞中无机械能损失.重力加速度为g.试求:
,碰撞中无机械能损失.重力加速度为g.试求:(1)待定系数β;
(2)第一次碰撞刚结束时小球A、B各自的速度和B球对轨道的压力;
(3)小球A、B在轨道最低处第二次碰撞刚结束时各自的速度,并讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度.
【答案】分析:(1)由题,碰撞中无机械能损失,以AB组成的系统研究,由机械能守恒定律研究A球从静止开始下滑到碰撞后A、B球达到的最大高度的过程,可求出待定系数β;
(2)碰撞后,A、B两球各自的机械能守恒,可求出碰撞后的速度,B球由轨道的支持力和重力的合力提供向心,由牛顿运动定律求解B球对轨道的压力;
(3)小球A、B在轨道最低处第二次碰撞过程,根据机械能守恒和动量守恒,求出小球A、B碰撞后两球的速度,再进行讨论.
解答:解:(1)A球从静止开始下滑到碰撞后A、B球达到的最大高度的过程,由机械能守恒定律得
mgR= mgR+
mgR+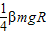
解得,β=3
(2)设A、B碰撞后的速度分别为v1、v2,则
则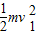 =
= mgR
mgR
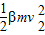 =
=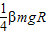
设向右方向正,向左为负,则得
v1=-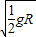 ,方向向左;
,方向向左;
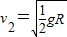 ,方向向右.
,方向向右.
设轨道对B球的支持力为N,B球对轨道的压力为N′,方向竖直向下为正
则由牛顿第二定律得
N-βmg=βm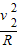
得,N=4.5mg
由牛顿第三定律得,N′=-N=-4.5mg,方向竖直向下.
(3)设A、B两球第二次碰撞刚结束时各自的速度分别为V1、V2,
由机械能守恒和动量守恒得
mgR=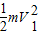 +
+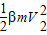
-mv1-βmv2=mV1+βmV2
解得,V1=-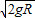 ,V2=0.(另一组解:V1=-v1,V2=-v2,不合题意,舍去)
,V2=0.(另一组解:V1=-v1,V2=-v2,不合题意,舍去)
由此可得
当n为奇数时,小球A、B在第n次碰撞铡结束时的速度分别与其第一次碰撞刚结束时相同;
当n为偶数时,小球A、B在第n次碰撞铡结束时的速度分别与其第二次碰撞刚结束时相同;
答:
(1)待定系数β是3.
(2)第一次碰撞刚结束时小球A、B各自的速度为-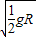 ,方向向左和
,方向向左和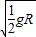 ,方向向右;B球对轨道的压力是4.5mg,方向竖直向下.
,方向向右;B球对轨道的压力是4.5mg,方向竖直向下.
(3)小球A、B在轨道最低处第二次碰撞刚结束时各自的速度分别是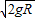 和0,当n为奇数时,小球A、B在第n次碰撞铡结束时的速度分别与其第一次碰撞刚结束时相同;
和0,当n为奇数时,小球A、B在第n次碰撞铡结束时的速度分别与其第一次碰撞刚结束时相同;
当n为偶数时,小球A、B在第n次碰撞铡结束时的速度分别与其第二次碰撞刚结束时相同;
点评:本题中两球发生弹性碰撞,遵守两大守恒:机械能守恒和动量守恒,要灵活选择研究对象和研究的过程,注意研究动量时,要选正方向,用正负号表示动量的方向.
(2)碰撞后,A、B两球各自的机械能守恒,可求出碰撞后的速度,B球由轨道的支持力和重力的合力提供向心,由牛顿运动定律求解B球对轨道的压力;
(3)小球A、B在轨道最低处第二次碰撞过程,根据机械能守恒和动量守恒,求出小球A、B碰撞后两球的速度,再进行讨论.
解答:解:(1)A球从静止开始下滑到碰撞后A、B球达到的最大高度的过程,由机械能守恒定律得
mgR=
 mgR+
mgR+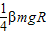
解得,β=3
(2)设A、B碰撞后的速度分别为v1、v2,则
则
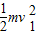 =
= mgR
mgR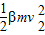 =
=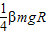
设向右方向正,向左为负,则得
v1=-
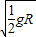 ,方向向左;
,方向向左;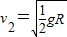 ,方向向右.
,方向向右.设轨道对B球的支持力为N,B球对轨道的压力为N′,方向竖直向下为正
则由牛顿第二定律得
N-βmg=βm
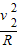
得,N=4.5mg
由牛顿第三定律得,N′=-N=-4.5mg,方向竖直向下.
(3)设A、B两球第二次碰撞刚结束时各自的速度分别为V1、V2,
由机械能守恒和动量守恒得
mgR=
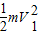 +
+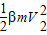
-mv1-βmv2=mV1+βmV2
解得,V1=-
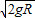 ,V2=0.(另一组解:V1=-v1,V2=-v2,不合题意,舍去)
,V2=0.(另一组解:V1=-v1,V2=-v2,不合题意,舍去)由此可得
当n为奇数时,小球A、B在第n次碰撞铡结束时的速度分别与其第一次碰撞刚结束时相同;
当n为偶数时,小球A、B在第n次碰撞铡结束时的速度分别与其第二次碰撞刚结束时相同;
答:
(1)待定系数β是3.
(2)第一次碰撞刚结束时小球A、B各自的速度为-
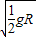 ,方向向左和
,方向向左和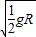 ,方向向右;B球对轨道的压力是4.5mg,方向竖直向下.
,方向向右;B球对轨道的压力是4.5mg,方向竖直向下.(3)小球A、B在轨道最低处第二次碰撞刚结束时各自的速度分别是
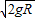 和0,当n为奇数时,小球A、B在第n次碰撞铡结束时的速度分别与其第一次碰撞刚结束时相同;
和0,当n为奇数时,小球A、B在第n次碰撞铡结束时的速度分别与其第一次碰撞刚结束时相同; 当n为偶数时,小球A、B在第n次碰撞铡结束时的速度分别与其第二次碰撞刚结束时相同;
点评:本题中两球发生弹性碰撞,遵守两大守恒:机械能守恒和动量守恒,要灵活选择研究对象和研究的过程,注意研究动量时,要选正方向,用正负号表示动量的方向.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
 如图,半径为R的光滑半球放在水平地面上,用跨过光滑小滑轮的细绳系一小球,小球质量为m,将小球搁在球面上,在拉力作用下,小球缓慢上升至半球体的顶点,在此过程中,小球对半球体的压力N和对细绳的拉力T的变化情况是( )
如图,半径为R的光滑半球放在水平地面上,用跨过光滑小滑轮的细绳系一小球,小球质量为m,将小球搁在球面上,在拉力作用下,小球缓慢上升至半球体的顶点,在此过程中,小球对半球体的压力N和对细绳的拉力T的变化情况是( ) 如图,半径为R的光滑圆形轨道安置在一竖直平面上,左侧连接一个光滑的弧形轨道,右侧连接动摩擦因数为μ的水平轨道CD.一小球自弧形轨道上端的A处由静止释放,通过圆轨道后,再滑上CD轨道.若在圆轨道最高点B处对轨道的压力恰好为零,到达D点时的速度为
如图,半径为R的光滑圆形轨道安置在一竖直平面上,左侧连接一个光滑的弧形轨道,右侧连接动摩擦因数为μ的水平轨道CD.一小球自弧形轨道上端的A处由静止释放,通过圆轨道后,再滑上CD轨道.若在圆轨道最高点B处对轨道的压力恰好为零,到达D点时的速度为 如图,半径为R的光滑圆形轨道固定在竖直面内.小球A、B质量分别为m、3m.A球从左边某高处由静止释放,并与静止于轨道最低点的B球相撞,碰撞后A球被反向弹回,且A、B球能达到的最大高度均为
如图,半径为R的光滑圆形轨道固定在竖直面内.小球A、B质量分别为m、3m.A球从左边某高处由静止释放,并与静止于轨道最低点的B球相撞,碰撞后A球被反向弹回,且A、B球能达到的最大高度均为 (2013?宿迁一模)如图,半径为R的光滑半圆形轨道ABC在竖直平面内,与水平轨道CD相切于C 点,D端有一被锁定的轻质压缩弹簧,弹簧左端连接在固定的挡板上,弹簧右端Q到C点的距离为2R.质量为m可视为质点的滑块从轨道上的P点由静止滑下,刚好能运动到Q点,并能触发弹簧解除锁定,然后滑块被弹回,且刚好能通过圆轨道的最高点A.已知∠POC=60°,求:
(2013?宿迁一模)如图,半径为R的光滑半圆形轨道ABC在竖直平面内,与水平轨道CD相切于C 点,D端有一被锁定的轻质压缩弹簧,弹簧左端连接在固定的挡板上,弹簧右端Q到C点的距离为2R.质量为m可视为质点的滑块从轨道上的P点由静止滑下,刚好能运动到Q点,并能触发弹簧解除锁定,然后滑块被弹回,且刚好能通过圆轨道的最高点A.已知∠POC=60°,求: (2009?汕头一模)如图,半径为R的光滑半圆面固定在竖直面内,其直径AB处于竖直方向上.一质量为m的小球以初速度v0从最低点A水平射入轨道并运动到最高点B处.则( )
(2009?汕头一模)如图,半径为R的光滑半圆面固定在竖直面内,其直径AB处于竖直方向上.一质量为m的小球以初速度v0从最低点A水平射入轨道并运动到最高点B处.则( )