题目内容
7. 如图所示,是一根长直实心圆柱玻璃棒横截面图,其两端是平面,且与轴线垂直.一束激光从与AB轴成某一角度θ的方向射入玻璃棒,若该玻璃棒的折射率为n,长为L,玻璃外都是空气.求:
如图所示,是一根长直实心圆柱玻璃棒横截面图,其两端是平面,且与轴线垂直.一束激光从与AB轴成某一角度θ的方向射入玻璃棒,若该玻璃棒的折射率为n,长为L,玻璃外都是空气.求:(i)如果激光束以任意角度从一端射入都能从另一端全部射出,则玻璃棒的折射率应满足什么关系?
(ii)当θ值变化时,光由玻璃棒的一端传播到另一端的时间范围.
分析 (1)若光从左端以与端面成30°入射,根据折射定律求出折射角,由几何知识求出光线在侧面上的入射角θ,与临界角C进行比较,若θ>C,将发生全反射,不能从侧面射出.
(2)由v=$\frac{c}{n}$求出光在玻璃管内的传播速度.由几何关系求出光通过的总路程s,由t=$\frac{s}{v}$求光通过玻璃管所需的时间.
解答 解:(1)光线射入左端时,n=$\frac{sinθ}{sinr}$,
恰好射入时:θ=90°
由几何关系得:光在侧面上的入射角β=90°-r
恰好不能射出时:β=C
其中:sinC=$\frac{1}{n}$,
联立可得:n=$\sqrt{2}$
可知,当玻璃的折射率大于等于$\sqrt{2}$时,光线在侧面上发生全反射不射出,光都能从另一端全部射出.
(2)光在玻璃管内的传播速度v=$\frac{c}{n}$,光在玻璃管通过的总路程s=$\frac{L}{cosγ}$.
则光通过玻璃管所需的时间t=$\frac{s}{v}$=$\frac{nL}{c•cosγ}$
当θ=0时,γ=0,则时间最短,为t=$\frac{nL}{c}$=$\frac{\sqrt{2}L}{c}$
当θ=90°时,γ=45°,则时间最长,为:t=$\frac{nL}{c•cosγ}$=$\frac{2L}{c}$
答:(i)如果激光束以任意角度从一端射入都能从另一端全部射出,则玻璃棒的折射率应大于等于$\sqrt{2}$;
(ii)当θ值变化时,光由玻璃棒的一端传播到另一端的时间范围是[$\frac{\sqrt{2}L}{c}$,$\frac{2L}{c}$].
点评 本题考查了光的全反射的知识.对于全反射是考试的热点,要掌握产生全反射的条件:光必须从光密介质进入光疏介质,同时入射角大于临界角.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| A. | 石块的质量m | B. | 石块初速度v0的大小 | ||
| C. | 石块抛出时的仰角θ | D. | 石块抛出时的离地高度h |
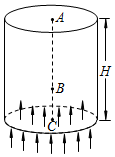 “娱乐风洞”是一项将科技与惊险相结合的娱乐项目,它能在一个特定的空间内把表演者“吹”起来.假设风洞内向上的风量和风速保持不变,表演者调整身体的姿态,通过改变受风面积(表演者在垂直风力方向的投影面积),来改变所受向上风力的大小.已知人体所受风力大小与受风面积成正比.人水平横躺时受风面积最大,此时人所受风力大于重力;站立时受风面积最小,此时人所受风力小于重力;如图所示,某次表演中,人体可上下移动的空间总高度为H,表演者由静止以站立身姿从A位置下落,经过B位置时调整为水平横躺身姿(不计调整过程的时间和速度变化),运动到C位置速度恰好减为零.已知AB段距离大于BC段距离,关于表演者下落的过程,下列说法正确的是( )
“娱乐风洞”是一项将科技与惊险相结合的娱乐项目,它能在一个特定的空间内把表演者“吹”起来.假设风洞内向上的风量和风速保持不变,表演者调整身体的姿态,通过改变受风面积(表演者在垂直风力方向的投影面积),来改变所受向上风力的大小.已知人体所受风力大小与受风面积成正比.人水平横躺时受风面积最大,此时人所受风力大于重力;站立时受风面积最小,此时人所受风力小于重力;如图所示,某次表演中,人体可上下移动的空间总高度为H,表演者由静止以站立身姿从A位置下落,经过B位置时调整为水平横躺身姿(不计调整过程的时间和速度变化),运动到C位置速度恰好减为零.已知AB段距离大于BC段距离,关于表演者下落的过程,下列说法正确的是( )| A. | 从A至B过程表演者的平均速度大于从B至C过程表演者的平均速度 | |
| B. | 从A至B过程表演者的运动时间等于从B至C过程表演者的运动时间 | |
| C. | 从A至B过程表演者加速度的绝对值大于从B至C过程表演者加速度的绝对值 | |
| D. | 从A至C的过程中,重力对表演者做的功等于表演者克服风力做的功 |
 如图所示,Q1:Q2为两个固定的点电荷,其中Q1带正电,Q2带负电,且Q1>Q2,a、b、c三点在它们连线上,b为连线中点,ab=bc,则( )
如图所示,Q1:Q2为两个固定的点电荷,其中Q1带正电,Q2带负电,且Q1>Q2,a、b、c三点在它们连线上,b为连线中点,ab=bc,则( )| A. | b点电势最低 | B. | 质子由a运动到c,在a点电势能最大 | ||
| C. | 质子由a运动到c,在b点动能最大 | D. | ab间电势差等于bc间电势差 |
 等量、同种、带正电的点电荷的连线和其中垂线如图所示.一个带负电的试探电荷,先从图中a点沿直线移到b点,再从b点沿直线移到c点,则( )
等量、同种、带正电的点电荷的连线和其中垂线如图所示.一个带负电的试探电荷,先从图中a点沿直线移到b点,再从b点沿直线移到c点,则( )| A. | 试探电荷所受电场力的方向一直不变 | |
| B. | 试探电荷所受电场力的大小先减小后增大 | |
| C. | 试探电荷的电势能一直减小 | |
| D. | a、b、c三点电势为:φa<φb<φc |
 两电荷量分别为Q1和Q2的点电荷放在x 轴上的O、A 两点,两电荷连线上各点电势φ随x变化的关系如图所示,其中B、C 两点的电势均为零,则( )
两电荷量分别为Q1和Q2的点电荷放在x 轴上的O、A 两点,两电荷连线上各点电势φ随x变化的关系如图所示,其中B、C 两点的电势均为零,则( )| A. | Q1与Q2带异种电荷 | |
| B. | B、C 点的电场强度大小为零 | |
| C. | CD 点间各点的场强方向向x 轴负方向 | |
| D. | 若有一个电子在C 点无初速运动,则在随后的一段时间内,电场力先做正功后做负功 |
 在如图所示的闭合铁芯上绕有一组线圈,与滑动变阻器、电池构成闭合电路,a、b、c为三个闭合金属圆环,假定线圈产生的磁场全部集中在铁芯内,则当滑动变阻器的滑片向右滑动过程中,下列说法正确的是( )
在如图所示的闭合铁芯上绕有一组线圈,与滑动变阻器、电池构成闭合电路,a、b、c为三个闭合金属圆环,假定线圈产生的磁场全部集中在铁芯内,则当滑动变阻器的滑片向右滑动过程中,下列说法正确的是( )| A. | a、b两个环的磁通量始终相同 | B. | b环磁通量始终是c环的一半 | ||
| C. | a、c两个环中都有感应电流 | D. | b、c两环中都有感应电流 |
 如图,小球套在光滑的竖直杆上,轻弹簧一端固定于O点,另一端与小球相连,现将小球从M点由静止释放,下降过程中先经过与O等高的P点,然后到达下方的N点,已知小球经M、N点时,弹簧的压缩量与伸长量相等,小球质量为m,重力加速度为g.
如图,小球套在光滑的竖直杆上,轻弹簧一端固定于O点,另一端与小球相连,现将小球从M点由静止释放,下降过程中先经过与O等高的P点,然后到达下方的N点,已知小球经M、N点时,弹簧的压缩量与伸长量相等,小球质量为m,重力加速度为g.