题目内容
如图所示，一个可忽略重力不计的带电量为q微粒，从两偏转极板的中间点O垂直进入一个偏转电场．偏转电场两个极板所加电压为U，偏转板板的长度为L，两极板间的距离为d．求：（1）若微粒能穿出偏转电场，带电微粒穿过偏转电场所用的时间是多少？
（2）若微粒能穿出偏转电场，带电微粒的偏转位移y是多少？
（3）要使微粒能穿出偏转板，偏转电压U至少为多少？
【答案】分析：（1）（2）带电微粒在偏转电场中只受电场力作用，做类平抛运动，运用运动的分解法研究：在水平方向微粒做匀速直线运动，在竖直方向做匀加速直线运动，根据牛顿第二定律和运动学公式结合求解时间和偏转位移y．
（3）微粒恰好从下边缘飞出电场时，此时偏转的距离为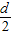
，牛顿第二定律和运动学公式结合求解U的最小值．
解答：解：（1）带电微粒在偏转电场中只受电场力作用，做类平抛运动．在水平方向微粒做匀速直线运动．
带电微粒穿过偏转电场所用的时间是 t=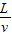
（2）带电微粒在竖直方向做匀加速直线运动，加速度为a，出电场时竖直方向速度为v2
竖直方向：a=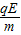
=
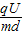
带电微粒的偏转位移y=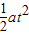
=
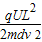
（3）微粒恰好从下边缘飞出电场时，此时偏转的距离为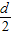
，
则有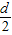
=
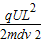
解得，U=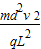
故要使微粒能穿出偏转板，偏转电压U至少为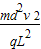
．
答：（1）若微粒能穿出偏转电场，带电微粒穿过偏转电场所用的时间是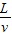
．
（2）若微粒能穿出偏转电场，带电微粒的偏转位移y为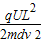
．
（3）要使微粒能穿出偏转板，偏转电压U至少为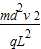
．
点评：本题的解题关键是掌握类平抛运动的分解方法：水平方向匀速直线运动，竖直方向初速度为零的匀加速直线运动，根据牛顿第二定律和运动学公式结合进行求解．
（3）微粒恰好从下边缘飞出电场时，此时偏转的距离为
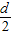，牛顿第二定律和运动学公式结合求解U的最小值．解答：解：（1）带电微粒在偏转电场中只受电场力作用，做类平抛运动．在水平方向微粒做匀速直线运动．
带电微粒穿过偏转电场所用的时间是 t=
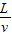
（2）带电微粒在竖直方向做匀加速直线运动，加速度为a，出电场时竖直方向速度为v2
竖直方向：a=
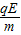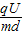
=带电微粒的偏转位移y=
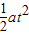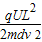
=（3）微粒恰好从下边缘飞出电场时，此时偏转的距离为
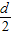，则有
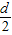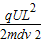
=解得，U=
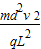
故要使微粒能穿出偏转板，偏转电压U至少为
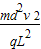．答：（1）若微粒能穿出偏转电场，带电微粒穿过偏转电场所用的时间是
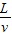．（2）若微粒能穿出偏转电场，带电微粒的偏转位移y为
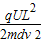．（3）要使微粒能穿出偏转板，偏转电压U至少为
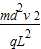．点评：本题的解题关键是掌握类平抛运动的分解方法：水平方向匀速直线运动，竖直方向初速度为零的匀加速直线运动，根据牛顿第二定律和运动学公式结合进行求解．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
相关题目
在空间中取坐标系Oxy，在第一象限内平行于y轴的虚线MN与y轴距离为d，从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场，电场强度大小为E，如图所示．初速可忽略的电子经过一个电势差U0未确定的电场直线加速后，从y轴上的A点以平行于x轴的方向射入第一象限区域，A点坐标为（0，h）．不计电子的重力．
如图所示，一个可忽略重力不计的带电量为q微粒，从两偏转极板的中间点O垂直进入一个偏转电场．偏转电场两个极板所加电压为U，偏转板板的长度为L，两极板间的距离为d．求：
在空间中取坐标系Oxy，在第一象限内平行于y轴的虚线MN与y轴距离为d，从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场，电场强度大小为E，如图所示．初速可忽略的电子经过一个电场直线加速后，从y轴上的A点以平行于x轴的方向射入第一象限区域，A点坐标为（0，h）．已知电子带电量大小e，质量m，忽略电子重力的作用．