题目内容
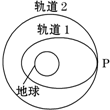（2010?德州一模）我国于2010年1月17日凌晨在西昌成功发射第三颗北斗导航卫星，此前，我国已成功发射了两颗北斗导航卫星，这次发射的北斗导航卫星（COMPASS-G2）是一颗地球同步卫星．如图所示，假若第三颗北斗导航卫星先沿椭圆轨道1飞行，后在远地点P处点火加速，由椭圆轨道1变成地球同步圆轨道2．下列说法正确的是（ ）分析：根据万有引力提供向心力得出线速度与轨道半径的大小关系，从而比较出卫星在轨道2上运行的速度与第一宇宙速度的关系．根据a=rω2，比较卫星在轨道2上的向心加速度与赤道上静止物体的向心加速度大小．根据万有引力的大小，通过牛顿第二定律比较加速度的大小．
解答：解：A、根据G
=m
知，v=
，轨道半径越大，线速度越小，第一宇宙速度的轨道半径等于地球的半径，则卫星在轨道2上运行的速度小于7.9km/s．故A错误．
B、卫星在轨道2上受重力作用．故B错误．
C、因为卫星在同步轨道上的角速度与地球自转的角速度相等，根据a=rω2知，卫星在轨道2运行时的向心加速度大于在赤道上相对地球静止的物体的向心加速度．故C错误．
D、卫星在轨道1上经过P点和轨道2上经过P点所受的万有引力大小相等，根据牛顿第二定律知加速度大小相等．故D正确．
故选D．
| mM |
| r2 |
| v2 |
| r |
|
B、卫星在轨道2上受重力作用．故B错误．
C、因为卫星在同步轨道上的角速度与地球自转的角速度相等，根据a=rω2知，卫星在轨道2运行时的向心加速度大于在赤道上相对地球静止的物体的向心加速度．故C错误．
D、卫星在轨道1上经过P点和轨道2上经过P点所受的万有引力大小相等，根据牛顿第二定律知加速度大小相等．故D正确．
故选D．
点评：解决本题的关键知道同步卫星的特点，以及掌握万有引力提供向心力这一理论，并能灵活运用．
练习册系列答案
相关题目
（2010?德州一模）如图所示，真空中有两个等量异种点电荷A、B，M、N、O是AB连线的垂线上的点，且AO＞OB．一带负电的试探电荷仅受电场力作用，运动轨迹如图中实线所示，设M、N两点的场强大小分别EM、EN，电势分别为φM、φN．下列判断中正确的是（ ）
（2010?德州一模）2009年是中华人民共和国成立60周年，南莫中学物理兴趣小组用空心透明塑料管制作了如图所示的竖直“60”造型．两个“0”字型的半径均为R．让一质量为m、直径略小于管径的光滑小球从入口A处射入，依次经过图中的B、C、D三点，最后从E点飞出．已知BC是“0”字型的一条直径，D点是该造型最左侧的一点，当地的重力加速度为g，不计一切阻力，则小球在整个运动过程中（ ）
（2010?德州一模）如图所示，一个截面为直角三角形的三棱镜，∠A=30°，∠C=90°．三棱镜材料的折射率n=