某校为了探索一种新的教学模式,进行了一项课题实验,甲班为实验班,乙班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,测试成绩的分组区间为[80,90)、[90,100)、[100,110)、[110,120)、[120,130),由此得到两个班测试成绩的频率分布直方图:

(Ⅰ)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
(Ⅱ)现从乙班50人中任意抽取3人,记ξ表示抽到测试成绩在[100,120)的人数,求ξ的分布列和数学期望Eξ.
附:K2= ,其中n=a+b+c+d
,其中n=a+b+c+d
0 77716 77724 77730 77734 77740 77742 77746 77752 77754 77760 77766 77770 77772 77776 77782 77784 77790 77794 77796 77800 77802 77806 77808 77810 77811 77812 77814 77815 77816 77818 77820 77824 77826 77830 77832 77836 77842 77844 77850 77854 77856 77860 77866 77872 77874 77880 77884 77886 77892 77896 77902 77910 266669

(Ⅰ)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
| 成绩小于100分 | 成绩不小于100分 | 合计 | |
| 甲班 | a=______ | b=______ | 50 |
| 乙班 | c=24 | d=26 | 50 |
| 合计 | e=______ | f=______ | 100 |
附:K2=
 ,其中n=a+b+c+d
,其中n=a+b+c+d| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.204 | 6.635 | 7.879 | 10.828 |
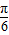 )+2sin2
)+2sin2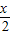 .
. ,△ABC的面积S=
,△ABC的面积S=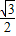 ,a=
,a=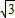 ,求sinB+sinC的值.
,求sinB+sinC的值. 已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.
已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点. ,试证明:对任意两个不相等正数x1、x2,不等式
,试证明:对任意两个不相等正数x1、x2,不等式 恒成立.
恒成立. +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+ =0相切.
=0相切. (O为坐标原点),当|
(O为坐标原点),当| -
- |<
|< 时,求实数t取值范围.
时,求实数t取值范围. 在复平面上对应的点位于( )
在复平面上对应的点位于( ) ,则
,则 =( )
=( )

 的渐近线方程为( )
的渐近线方程为( )



