(本小题满分12分)
某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(学历)的调查,其结果(人数
分布)如下表:
| 学历 | 35岁以下 | 35~50岁 | 50岁以上 |
| 本科 | 80 | 30 | 20 |
| 研究生 |  | 20 |  |
看成一个总体, 从中任取2人, 求至少有1人的学历为研究生的概率;
(2)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取
 个人,其中35岁以
个人,其中35岁以下48人,50岁以上10人,再从这
 个人中随机抽取出1人,此人的年龄为50岁以上
个人中随机抽取出1人,此人的年龄为50岁以上的概率为
 ,求
,求 、
、 的值.
的值. (本题满分14分).对某电子元件进行寿命追踪调查,情况如下.
| 寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个 数 | 20 | 30 | 80 | 40 | 30 |
(1)列出频率分布表;
(2)画出频率分布直方图;
(3)估计电子元件寿命在100~400 h以内的在总体中占的比例;
(4)估计电子元件寿命在400 h以上的在总体中占的比例.
(本小题满分12分)某校高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | | 0.050 |
| [105,115) | | 0.200 |
| [115,125) | 12 | 0.300 |
| [125,135) | | 0.275 |
| [135,145) | 4 | ③ |
| [145,155) | | 0.050 |
| 合计 | | ④ |

(1)根据上面图表,①②③④处的数值分别为________、________、________、________;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在[129,155]中的频率.
 (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
(吨)与相应的生产能耗y(吨标准煤)的几组对应数据. 所表示的直线必经过的点;
所表示的直线必经过的点; ;
; )
) ,
, ,…,
,…, .后画出如下部分频率分布直方图.观察图形的信息,回答下列题:
.后画出如下部分频率分布直方图.观察图形的信息,回答下列题: 分的学生中选两人,求他们在同一分数段的概率.
分的学生中选两人,求他们在同一分数段的概率. ,求
,求 .
.
 一样大?从中你能
一样大?从中你能 发现什么样的一般规律?(直接写出结论,不必证明)(2)求至少出现一次5点或6点的概率
发现什么样的一般规律?(直接写出结论,不必证明)(2)求至少出现一次5点或6点的概率 中位数约是多少?(精确到0.01)
中位数约是多少?(精确到0.01)
 生参加英语口语测试,其中男生250名,女生200名。现按性别用分层抽样的方法从中抽取45名学生的成绩。
生参加英语口语测试,其中男生250名,女生200名。现按性别用分层抽样的方法从中抽取45名学生的成绩。

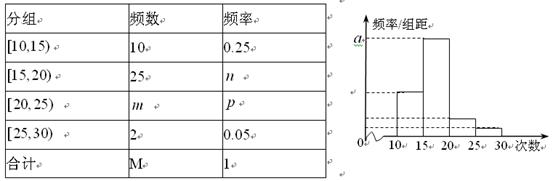
 及图中
及图中 的值;
的值;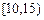 内的人数;
内的人数; 内的概率.
内的概率.