用反证法证明:“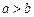 ”,应假设为( ).
”,应假设为( ).

A.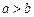 高*考*资*源*网 高*考*资*源*网 | B.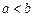 | C.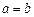 | D.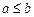 |
设 ,则下列不等式中恒成立的是( )
,则下列不等式中恒成立的是( )
A. | B. |
C. | D. |
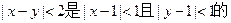 ( )
( )
| A.充分不必要条件 | B.必要不充分条件 |
C.充要条件 | D.既不充分也不必要条件 |
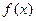 ,
, 分别是定义在
分别是定义在 上的奇函数和偶函数,当
上的奇函数和偶函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-∞,-3)∪(3,+∞) | C.(-∞,-3)∪(0,3) | D.(-3,0)∪(0,3) 中学学科网 |
若关于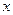 的不等式
的不等式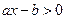 的解集是
的解集是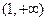 ,则关于
,则关于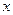 的不等式
的不等式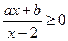 的解集是 ( )
的解集是 ( )
A.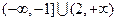 | B.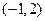 | C.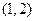 | D.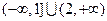 |
已知 ,则下列不等式恒成立的是( )
,则下列不等式恒成立的是( )
A. | B. | C. | D. |
有四个命题:①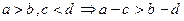 ;②
;②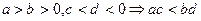 ③
③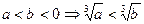 ;④
;④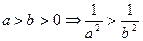 ;⑤若
;⑤若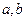 为实数,则
为实数,则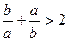 其中命题正确的有( )个 高☆考♂资♀源?网
其中命题正确的有( )个 高☆考♂资♀源?网
| A.2 | B.3 | C.4 | D.5 |
二次不等式 的解集是全体实数的条件是
的解集是全体实数的条件是
A. | B. | C. | D. |
已知不等式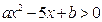 的解集是
的解集是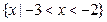 ,则不等式
,则不等式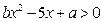 的
的
解是( )
A.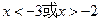 | B.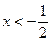 或 或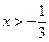 | C.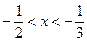 | D.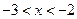 |
有四个命题:①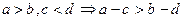 ;②
;②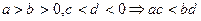 ③
③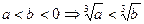 ;④
;④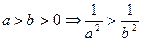 ;⑤若
;⑤若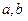 为实数,则
为实数,则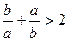 其中命题正确的有( )个
其中命题正确的有( )个
高☆考♂资♀源?网
| A.2 | B.3 | C.4 | D.5 |