数列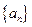 满足
满足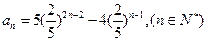 ,若
,若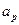 和
和 分别为数列中的最大项和最小项,则
分别为数列中的最大项和最小项,则 =(★)
=(★)
| A.3 | B.4 | C.5 | D.6 |
等比数列{an}的公比q>1,且第17项的平方等于该数列的第24项的值,则使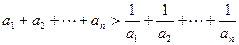 成立的最小自然数n是( )
成立的最小自然数n是( )
| A.10 | B.11 | C.19 | D.20 |
设数列 满足
满足 ,
, ,通过求
,通过求 ,
, 猜想
猜想 的一个通项公式为( )
的一个通项公式为( )
A. | B. | C. | D. |
观察式子: …,
…,
可归纳出式子( )
A. | B. | C. | D. |
(理科)已知数列 、
、 都是公差为1的等差数列,其首项分别为
都是公差为1的等差数列,其首项分别为 、
、 ,且
,且 ,
, ,
, ,则数列
,则数列 前10项的和等于( )
前10项的和等于( )
| A.55 | B.70 | C.85 | D.100 |
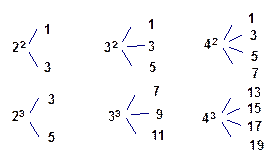
对于大于1的自然数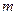 的
的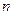 次幂可用奇数进行如图所示的“分裂”,仿此,记
次幂可用奇数进行如图所示的“分裂”,仿此,记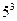 的“分裂”中的最小数为
的“分裂”中的最小数为 ,而
,而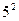 的“分裂”中最大的数是
的“分裂”中最大的数是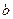 ,则
,则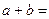
| A.30 | B.26 |
| C.32 | D.36 |
设 ,若
,若 成等差数列,
成等差数列, 成等比数列,则
成等比数列,则 的最小值为
的最小值为
A. | B. | C. | D. |
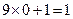 ,
,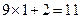 ,
,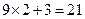 ,
,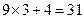 ,
, ,猜想第
,猜想第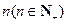 个等式应为
个等式应为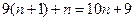 B.
B.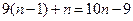

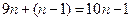 D.
D.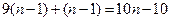
 个图中有
个图中有 根火柴棒,第
根火柴棒,第 个图中有
个图中有 根火柴棒,则在第
根火柴棒,则在第 个图中有火柴棒( ﹡ ).
个图中有火柴棒( ﹡ ). 
 根
根 根
根 根
根 根
根 的“均倒数”,数列
的“均倒数”,数列 的各项均为正数,且其前
的各项均为正数,且其前 项的“均倒数”为
项的“均倒数”为 ,则数列
,则数列


