极坐标方程ρcosθ=2sin2θ表示的曲线为( )
|
| A. | 一条射线和一个圆 | B. | 两条直线 |
|
| C. | 一条直线和一个圆 | D. | 一个圆 |
若直线的参数方程为![]() (t为参数),则直线的斜率为( )
(t为参数),则直线的斜率为( )
|
| A. |
| B. |
| C. |
| D. |
|
在极坐标表中,曲线ρ=4cosθ上任意两点间的距离的最大值为( )
|
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
科研室的老师为了研究某班学生数学成绩x与英语成绩y的相关性,对该班全体学生的某次期末检测的数学成绩和英语成绩进行统计分析,利用相关系数公式r=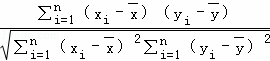 ,计算得r=﹣0.001,并且计算得到线性回归方程为y=bx+a,其中b=
,计算得r=﹣0.001,并且计算得到线性回归方程为y=bx+a,其中b=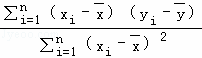 ,a=
,a=![]() .由此得该班全体学生的数学成绩x与英语成绩y相关性的下列结论正确的是( )
.由此得该班全体学生的数学成绩x与英语成绩y相关性的下列结论正确的是( )
|
| A. | 相关性较强且正相关 | B. | 相关性较弱且正相关 |
|
| C. | 相关性较强且负相关 | D. | 相关性较弱且负相关 |
如图所示程序框图运行后输出的结果为( )
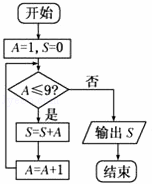
|
| A. | 36 | B. | 45 | C. | 55 | D. | 56 |
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x﹣85.71,则下列结论中不正确的是( )
=0.85x﹣85.71,则下列结论中不正确的是( )
|
| A. | y与x具有正的线性相关关系 |
|
| B. | 回归直线过样本点的中心( |
|
| C. | 若该大学某女生身高增加1cm,则其体重约增加0.85kg |
|
| D. | 若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为( )
|
| A. |
| B. |
| C. |
| D. |
|
法国数学家费马观察到![]() ,
,![]() ,
,![]() ,
,![]() 都是质数,于是他提出猜想:任何形如
都是质数,于是他提出猜想:任何形如![]() N*)的数都是质数,这就是著名的费马猜想.半个世纪之后,善于发现的欧拉发现第5个费马数
N*)的数都是质数,这就是著名的费马猜想.半个世纪之后,善于发现的欧拉发现第5个费马数![]() 不是质数,从而推翻了费马猜想,这一案例说明( )
不是质数,从而推翻了费马猜想,这一案例说明( )
|
| A. | 归纳推理,结果一定不正确 | B. | 归纳推理,结果不一定正确 |
|
| C. | 类比推理,结果一定不正确 | D. | 类比推理,结果不一定正确 |
设a,b∈R,i是虚数单位,则“ab=0”是“复数![]() 为纯虚数”的( )
为纯虚数”的( )
|
| A. | 充分不必要条件 | B. | 必要不充分条件 |
|
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
复数z=![]() 的共轭复数是( )
的共轭复数是( )
|
| A. | 2+i | B. | 2﹣i | C. | ﹣1+i | D. | ﹣1﹣i |