B. 
C.
D. 
B. 
C. 
D.
A、B两个代表队进行乒乓球对抗赛，每队三名队员，A队队员是A1、A2、A3，B队队员是B1、B2、B3，按以往多次比赛的统计，对阵队员之间胜负概率如下：
对阵队员 | A队队员胜的概率 | A队队员负的概率 |
A1对B1 |
|
|
A2对B2 |
|
|
A3对B3 |
|
|
现按表中对阵方式出场，每场胜队得1分，负队得0分.设A队、B队最后所得总分分别为ξ、η.
(1)求ξ、η的概率分布；
(2)求Eξ、Eη.
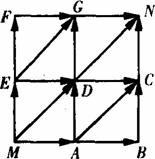
某商店老板设计了如下有奖游戏方案：顾客只要花10元钱，即可参加有奖游戏一次.游戏规则如下：在图示的棋盘中，棋子从M开始沿箭头方向跳向N，每次只跳一步(一个箭头)，当下一步有方向选择时，则必须通过掷一次骰子(每个面分别标有1，2，3，4，5，6的正方体玩具)的方法来确定(否则，不必掷骰子)——当出现“1”朝上时，沿MD方向跳；当出现“2，4，6”朝上时沿ME的方向跳；当出现“3”“5”朝上时，沿MA方向跳.奖励标准如下表：
从M到N所用步数 | 2 | 3 | 4 |
奖金(元) | 100 | 10 | 5 |
若该店平均每天有100人次参加游戏，按每月30天计.
(Ⅰ)写出每位顾客一次游戏后，该店获利的分布列；
(Ⅱ)该店开展此项游戏每月大约获利多少元?(精确到1元)
(1)如果随机试验的结果可以用一个________来表示，那么这样的________叫做随机变量；按一定次序一一列出，这样的随机___________叫做离散型随机_________；随机变量可以取某一区间内的__________,这样的随机变量叫做____________.?
0 56874 56882 56888 56892 56898 56900 56904 56910 56912 56918 56924 56928 56930 56934 56940 56942 56948 56952 56954 56958 56960 56964 56966 56968 56969 56970 56972 56973 56974 56976 56978 56982 56984 56988 56990 56994 57000 57002 57008 57012 57014 57018 57024 57030 57032 57038 57042 57044 57050 57054 57060 57068 266669
(2)设离散型随机变量ξ可能取的值为x1,x2,…，xi,…，ξ取每一个值xi(i=1,2，…，n,…)的概率P(ξ=xi)=pi,则称表
ξ | x1 | x2 | … | xi | … |
P | p1 | ____ | … | ____ | … |
? 为随机变量ξ的概率分布.具有性质：①pi______,i=1,2,…,n,…;②p1+p2+…+pn+…=_________.
离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率_______.?
(3)二项分布：如果在一次试验中某事件发生的概率是p，那么在n次独立重复试验中这个事件恰好发生k次的概率是P(ξ=k)=_______，其中k=0,1,2,3,…,n，q=1-p.于是得到随机变量ξ的概率分布如下：
ξ | 0 | 1 | … | k | … | n |
P |
| C1np1qn-1 | … | ____ | … |
|
p0qn
pnq0由于
pkqn-k恰好是二项展开式(q+p)n=
p0qn+
p1qn-1+…+________+…+
pnq0中的第k+1项(k=0,1,2,…,n)中的各个值，故称为随机变量ξ的二项分布，记作ξ～B(n,p).