题目内容
某商店老板设计了如下有奖游戏方案:顾客只要花10元钱,即可参加有奖游戏一次.游戏规则如下:在图示的棋盘中,棋子从M开始沿箭头方向跳向N,每次只跳一步(一个箭头),当下一步有方向选择时,则必须通过掷一次骰子(每个面分别标有1,2,3,4,5,6的正方体玩具)的方法来确定(否则,不必掷骰子)——当出现“1”朝上时,沿MD方向跳;当出现“2,4,6”朝上时沿ME的方向跳;当出现“3”“5”朝上时,沿MA方向跳.奖励标准如下表: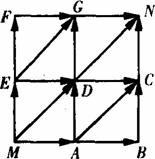
从M到N所用步数 | 2 | 3 | 4 |
奖金(元) | 100 | 10 | 5 |
若该店平均每天有100人次参加游戏,按每月30天计.
(Ⅰ)写出每位顾客一次游戏后,该店获利的分布列;
(Ⅱ)该店开展此项游戏每月大约获利多少元?(精确到1元)
解:(Ⅰ)设一位顾客参加一次游戏后,小商店获利为ξ元∴ξ分布列为:
ξ | -90 | 0 | 5 |
从M到N所用步数 | 2 | 3 | 4 |
P | P1 | P2 | P3 |
当ξ=-90时,只有一种跳棋路线M→D→N
P1=![]()
当ξ=0,有如下跳棋路线
M→D→C→N M→D→C→N M→A→D→N
M→E→D→N M→A→C→N M→E→C→N
∴P2=![]()
∴P3=![]()
(Ⅱ)∴Eξ=-90×![]() (元)
(元)
∴小商店每月获利大约有![]() ×100×30=
×100×30=![]() ≈2 083(元).
≈2 083(元).

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目