已知函数y=xlnx，则其在点x=e处的切线方程是（ ）
| A、y=2x-e | B、y=e | C、y=x-e | D、y=x+e |
已知f（x），g（x）都是定义在R上的函数，且满足以下条件：
①f(x)=
（a＞0，且a≠1）；
②g（x）≠0；
③f（x）?g′（x）＞f′（x）?g（x）．
若
+
=
，则a等于（ ）
①f(x)=
| g(x) |
| ax |
②g（x）≠0；
③f（x）?g′（x）＞f′（x）?g（x）．
若
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
D、2或
|
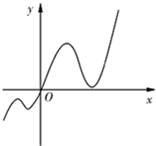定义在R上的函数f（x）的导函数f′（x）的图象如图，若两个正数a，b满足f（2a+b）＜1，且f（4）=1，则| b+1 |
| a+1 |
A、（
| ||||
B、（-∞，
| ||||
| C、（-∞，3） | ||||
D、（
|
下列求导运算正确的是（ ）
A、（
| ||||
B、（
| ||||
| C、（x2cosx）′=-2xsinx | ||||
D、（log2x）′=
|
定义方程f（x）=f′（x）（f′（x）是f（x）的导函数）的实数根x0叫做函数的f（x）“新驻点”，若函数g（x）=x，r（x）=ln（x+1），φ（x）=x3-1的“新驻点”分别为α，β，γ，则α，β，γ的大小关系为（ ）
| A、α＞β＞γ | B、β＞α＞γ | C、β＞γ＞α | D、γ＞α＞β |
已知曲线y=
-3lnx的一条切线的斜率为-
，则切点的横坐标为（ ）
| x2 |
| 4 |
| 1 |
| 2 |
| A、3 | ||
| B、2 | ||
| C、1 | ||
D、
|