题目内容
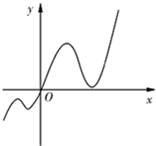定义在R上的函数f（x）的导函数f′（x）的图象如图，若两个正数a，b满足f（2a+b）＜1，且f（4）=1，则| b+1 |
| a+1 |
A、（
| ||||
B、（-∞，
| ||||
| C、（-∞，3） | ||||
D、（
|
分析：根据导数和函数单调性之间的关系确定函数的单调性，将不等式转化为线性规划问题即可求出结论．
解答：解：由图象可知f（x）在（-∞，0）递减，在（0，+∞）递增，
∵两个正数a，b满足f（2a+b）＜1，且f（4）=1
∴2a+b＜4，
原题等价于
，求
的取值范围．
画出不等式组表示的可行区域，利用直线斜率的意义可得PA的斜率k=
=5，
PB的斜率k=
=
，
∴
∈（
，5），
故选：D．
∵两个正数a，b满足f（2a+b）＜1，且f（4）=1
∴2a+b＜4，
原题等价于
|
| b+1 |
| a+1 |
画出不等式组表示的可行区域，利用直线斜率的意义可得PA的斜率k=
| -1-4 |
| -1-0 |
PB的斜率k=
| -1-0 |
| -1-2 |
| 1 |
| 3 |
∴
| b+1 |
| a+1 |
| 1 |
| 3 |
故选：D．
点评：本题主要考查函数单调性和导数之间的关系，将条件转化为线性规划问题是解决本题的关键，要求熟练掌直线的斜率公式．
练习册系列答案
相关题目