已知函数f(x)在R上可导,且f(x)=x2+2xf′(2),则函数f(x)的解析式为( )
| A、f(x)=x2+8x | B、f(x)=x2-8x | C、f(x)=x2+2x | D、f(x)=x2-2x |
己知f′(x)为函数f(x)=x+
的导函数,则下列结论中正确的是( )
| 1 |
| x |
| A、?x0∈R,?x∈R且x≠0,f(x)≤f(x0) |
| B、?x0∈R,?x∈R且x≠0,f(x)≥f(x0) |
| C、?x0∈R,?x∈(x0,+∞),f′(x)<0 |
| D、?x0∈R,?x∈(x0,+∞),f′(x)>0 |
函数y=f(x)在x=x0处的导数f′(x0)的几何意义是( )
| A、在点x0处的斜率 | B、在点(x0,f(x0))处的切线与x轴所夹锐角的正切值 | C、在点(x0,f(x0))与点(0,0)连线的斜率 | D、曲线y=f(x)在点(xo,f(x0))处切线的斜率 |
阅读如图程序框图,如果输出i=4,那么空白的判断框中应填入的条件是( )


| A、S<10? | B、S<12? | C、S<14? | D、S<16? |

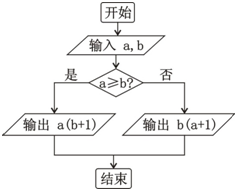 如图,定义某种运算S=a?b,运算原理如图所示,则式子(2tan
如图,定义某种运算S=a?b,运算原理如图所示,则式子(2tan 如图给出的是计算
如图给出的是计算 一个计算1+2+…+100的值的程序框图:在图中空缺处添上合适的内容.
一个计算1+2+…+100的值的程序框图:在图中空缺处添上合适的内容.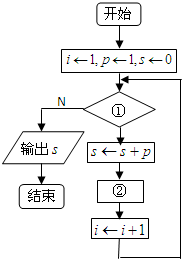 已知数列{an}满足:a1=1,an+1=an+n,数列{an}的前n项和为Sn.
已知数列{an}满足:a1=1,an+1=an+n,数列{an}的前n项和为Sn. 根据如图所示的程序框图,将输出的x,y依次记为x1,x2,…,x2003,y1,y2…y2013,
根据如图所示的程序框图,将输出的x,y依次记为x1,x2,…,x2003,y1,y2…y2013,