设三组实验数据(x1,y1).(x2,y2).(x3,y3)的回归直线方程是:y=bx+a,使代数式[y1-(bx1+a)]2+[y2-(bx2+a)]2+[y3-(bx3+a)]2的值最小时,a=
-b
,b=
,(
、
分别是这三组数据的横、纵坐标的平均数)
若有七组数据列表如图:
(Ⅰ)求上表中前三组数据的回归直线方程;
(Ⅱ)若|yi-(bxi+a)|≤0.2,即称(xi,yi)为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
0 33004 33012 33018 33022 33028 33030 33034 33040 33042 33048 33054 33058 33060 33064 33070 33072 33078 33082 33084 33088 33090 33094 33096 33098 33099 33100 33102 33103 33104 33106 33108 33112 33114 33118 33120 33124 33130 33132 33138 33142 33144 33148 33154 33160 33162 33168 33172 33174 33180 33184 33190 33198 266669
. |
| y |
. |
| x |
x1y1+x2y2+x3y3-3
| ||||
x12+x22+x32-3
|
. |
| x |
. |
| y |
若有七组数据列表如图:
| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 | 8.6 |
(Ⅱ)若|yi-(bxi+a)|≤0.2,即称(xi,yi)为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
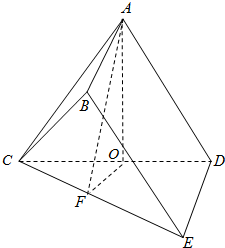 已知多面体ABCDE中,AB⊥平面ACD,DE∥AB,AB=1,AC=AD=CD=DE=2,F、O分别为CE、CD的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE∥AB,AB=1,AC=AD=CD=DE=2,F、O分别为CE、CD的中点.