在等腰Rt△ABC中,∠A=90°,
=(1,2),
=(m,n),则
=( )
| AB |
| AC |
| BC |
| A、(0,-4)或(-2,0) |
| B、(0,4)或(2,0) |
| C、(0,-4) |
| D、(-2,0) |
杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律.如图是一个11阶杨辉三角:
(1)求第20行中从左到右的第4个数;
(2)若第n行中从左到右第14与第15个数的比为
,求n的值;
(3)求n阶(包括0阶)杨辉三角的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.试用含有m、k(m,k∈N×)的数学公式表示上述结论,并给予证明.
0 32394 32402 32408 32412 32418 32420 32424 32430 32432 32438 32444 32448 32450 32454 32460 32462 32468 32472 32474 32478 32480 32484 32486 32488 32489 32490 32492 32493 32494 32496 32498 32502 32504 32508 32510 32514 32520 32522 32528 32532 32534 32538 32544 32550 32552 32558 32562 32564 32570 32574 32580 32588 266669
(1)求第20行中从左到右的第4个数;
(2)若第n行中从左到右第14与第15个数的比为
| 2 |
| 3 |
(3)求n阶(包括0阶)杨辉三角的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.试用含有m、k(m,k∈N×)的数学公式表示上述结论,并给予证明.
| 第0行 | 1 | … | … | … | … | … | … | … | … | … | … | … | … | 第1斜列 | |||||||||||
| 第1行 | 1 | 1 | … | … | … | … | … | … | … | … | … | … | … | 第2斜列 | |||||||||||
| 第2行 | 1 | 2 | 1 | … | … | … | … | … | … | … | … | … | … | 第3斜列 | |||||||||||
| 第3行 | 1 | 3 | 3 | 1 | … | … | … | … | … | … | … | … | … | 第4斜列 | |||||||||||
| 第4行 | 1 | 4 | 6 | 4 | 1 | … | … | … | … | … | … | … | … | 第5斜列 | |||||||||||
| 第5行 | 1 | 5 | 10 | 10 | 5 | 1 | … | … | … | … | … | … | … | 第6斜列 | |||||||||||
| 第6行 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | … | … | … | … | … | … | 第7斜列 | |||||||||||
| 第7行 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | … | … | … | … | … | 第8斜列 | |||||||||||
| 第8行 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | … | … | … | … | 第9斜列 | |||||||||||
| 第9行 | 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | … | … | … | 第10斜列 | |||||||||||
| 第10行 | 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | … | … | 第11斜列 | |||||||||||
| 第11行 | 1 | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 1 | … | 第12斜列 | |||||||||||
| 11阶杨辉三角 | |||||||||||||||||||||||||
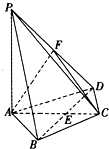 已知PA⊥平面ABCD,PA=AB=AD=2,AC与BD交于E点,BD=2,BC=CD.
已知PA⊥平面ABCD,PA=AB=AD=2,AC与BD交于E点,BD=2,BC=CD.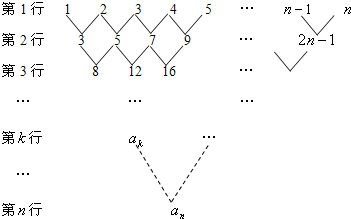
 如图,用一块形状为半椭圆
如图,用一块形状为半椭圆