已知A、B、C是△ABC的内角，向量
m
=(-1，
3
)，
n
=(cosA，sinA)，且
m
•
n
=1．
（1）求角A；
（2）若a=
3
，S△ABC=
3
2
，求b和c的值．
甲与乙进行一场乒乓球单打比赛时，甲获胜的局数ξ的期望Eξ=2，每场比赛打满3局．在三场比赛中，至少有两场比赛甲胜1局或2局的概率为
 
．
一个与球心距离为1的平面截球所得的圆面面积为π，则该球的表面积是
 
．
(
x
+
2
3x
)n的展开式中，只有第9项的二项式系数最大，则展开式中含x3的项是第
 
项．
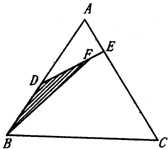
精英家教网如图所示，已知D是面积为1的△ABC的边AB上的任一点，E是边AC上任一点，连接DE，F是线段DE上一点，连接BF，设
AD
=λ1
AB
，
AE
=λ2
AC
，
DF
=λ3
DE
，且λ2+λ3-λ1=
1
2
，则△BDF的面积S的最大值是（　　）
A、
1
2
B、
1
3
C、
1
4
D、
1
8
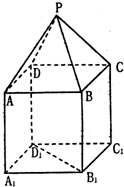精英家教网如图，P-ABCD是正四棱锥，ABCD-A1B1C1D1是正方体，其中AB=2，PA=
6
．平面PAD与平面BDD1B1所成的锐二面角θ的余弦值为（　　）
A、
10
10
B、
5
5
C、
15
5
D、
10
5
已知各项均不为零的数列{an}，定义向量
cn
=(an，an+1)，
bn
=(n，n+1)，n∈N*．下列命题中真命题是（　　）
A、若?n∈N*总有
cn
∥
bn
成立，则数列{an}是等差数列
B、若?n∈N*总有
cn
∥
bn
成立，则数列{an}是等比数列
C、若?n∈N*总有
cn
⊥
bn
成立，则数列{an}是等差数列
D、若?n∈N*总有
cn
⊥
bn
成立，则数列{an}是等比数列
7、某班有50名学生，其中正、副班长各1人，现选派5人参加一项活动，要求正、副班长至少有1人参加，问共有多少种选派方法？下面是学生提供的四种计算方法，其中错误的算法为（　　）
一个盒子中装有4张卡片，上面分别写着如下四个定义域为R的函数：f1（x）=x3，f2（x）=|x|，f3（x）=sinx，f4（x）=cosx，现从盒子中任取2张卡片，将卡片上的函数相乘得到一个新函数，所得函数为奇函数的概率是（　　）
A、
1
6
B、
1
3
C、
2
3
D、
5
6
关于函数f(x)=2sin(3x-
3π
4
)，有下列四个命题：
①其最小正周期为
2π
3
；
②其图象由y=2sin3x向左平移
π
4
个单位而得到；
③其表达式可以写成f(x)=2cos(3x+
3π
4
)；
④在x∈[
π
12
，
5π
12
]上为单调递增函数；则其中真命题为（　　）
A、①②④B、②③④
C、①③④D、①②③
 0  31990  31998  32004  32008  32014  32016  32020  32026  32028  32034  32040  32044  32046  32050  32056  32058  32064  32068  32070  32074  32076  32080  32082  32084  32085  32086  32088  32089  32090  32092  32094  32098  32100  32104  32106  32110  32116  32118  32124  32128  32130  32134  32140  32146  32148  32154  32158  32160  32166  32170  32176  32184  266669 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网