已知0≤a<2,0≤b<4,为估计在a>1的条件下,函数f(x)=x2+2ax+b有两相异零点的概率P.用计算机产生了[{0,1})内的两组随机数a1,b1各2400个,并组成了2400个有序数对(a1,b1),统计这2400个有序数对后得到2×2列联表的部分数据如下表:
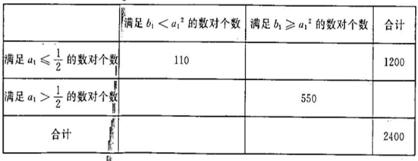
则数据表中数据计算出的概率P的估计值为( )

则数据表中数据计算出的概率P的估计值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知△ABP的顶点A、B分别为双曲线C:
-
=1的左、右焦点,顶点P在双曲线C上,则
的值等于( )
| x2 |
| 16 |
| y2 |
| 9 |
| |sinA-sinB| |
| sinP |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将函数y=sin(2x+
)的图象上各点的纵坐标不变,横坐标伸长到原来的2倍,再向右平移
个单位,所得到的图象解析式是( )
| π |
| 4 |
| π |
| 4 |
| A、f(x)=sinx |
| B、f(x)=cosx |
| C、f(x)=sin4x |
| D、f(x)=cos4x |
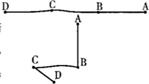 将长为3米的直铜线AD沿三等分点B、C折成三段(不断开),并使三线段AB、BC、CD所在直线两两垂直(如图)则三棱锥A-BCD的外接球的表面积为
将长为3米的直铜线AD沿三等分点B、C折成三段(不断开),并使三线段AB、BC、CD所在直线两两垂直(如图)则三棱锥A-BCD的外接球的表面积为
 13、某管理部门用问卷调查的方式对当地10000名中学生开展了“阳光冬季长跑”活动情况调查,x(单位:米)表示平均每天参加长跑的里程,现按长跑里程分下列四种情况进行统计:
13、某管理部门用问卷调查的方式对当地10000名中学生开展了“阳光冬季长跑”活动情况调查,x(单位:米)表示平均每天参加长跑的里程,现按长跑里程分下列四种情况进行统计: