已知函数f(x)=
(x∈R)时,则下列结论不正确的是( )
| x |
| 1+|x| |
| A、?x∈R,等式f(-x)+f(x)=0恒成立 |
| B、?m∈(0,1),使得方程|f(x)|=m有两个不等实数根 |
| C、?x1,x2∈R,若x1≠x2,则一定有f(x1)≠f(x2) |
| D、?k∈(1,+∞),使得函数g(x)=f(x)-kx在R上有三个零点 |
在区间[0,1]上任取两个实数a、b,则函数f(x)=
x3+ax-b在区间(-1,1)上有且仅有一个零点的概率为( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若
=-
,则sinα+cosα的值为( )
sin(α-
| ||
| cos2α |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
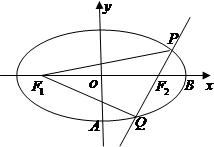 已知椭圆
已知椭圆 中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.济南市公安局交通管理部门于2011年2月的某天晚上8点至11点在市区设点进行一次拦查行动,共依法查出了60名饮酒后违法驾驶机动车者,如图,为这60名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内).
中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.济南市公安局交通管理部门于2011年2月的某天晚上8点至11点在市区设点进行一次拦查行动,共依法查出了60名饮酒后违法驾驶机动车者,如图,为这60名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内). 三棱锥P-ABC中,∠BAC=90°,PA=PB=PC=BC=2AB=2,
三棱锥P-ABC中,∠BAC=90°,PA=PB=PC=BC=2AB=2, 如图,一架飞机原计划从空中A处直飞相距680km的空中B处,为避开直飞途中的雷雨云层,飞机在A处沿与原飞行方向成θ角的方向飞行,在中途C处转向与原方向线成45°角的方向直飞到达B处.已
如图,一架飞机原计划从空中A处直飞相距680km的空中B处,为避开直飞途中的雷雨云层,飞机在A处沿与原飞行方向成θ角的方向飞行,在中途C处转向与原方向线成45°角的方向直飞到达B处.已 14、给出右面的程序框图,则输出的结果为
14、给出右面的程序框图,则输出的结果为