题目内容
 如图,一架飞机原计划从空中A处直飞相距680km的空中B处,为避开直飞途中的雷雨云层,飞机在A处沿与原飞行方向成θ角的方向飞行,在中途C处转向与原方向线成45°角的方向直飞到达B处.已sinθ=
如图,一架飞机原计划从空中A处直飞相距680km的空中B处,为避开直飞途中的雷雨云层,飞机在A处沿与原飞行方向成θ角的方向飞行,在中途C处转向与原方向线成45°角的方向直飞到达B处.已sinθ=| 5 |
| 13 |
(1)在飞行路径△ABC中,求tanC;
(2)求新的飞行路程比原路程多多少km.
(参考数据:
| 2 |
| 3 |
分析:(1)由θ角的正弦由平方关系得θ角余弦,进而得θ角正切,由三角形内角和得角C与θ角的关系,由诱导公式和两角和的正切公式得tanC;
(2)由三角形内角和得角C与θ角的关系,由诱导公式和两角和的正弦公式得sinC,由正弦定理得AC、BC的长度,进而得出要求的量.
(2)由三角形内角和得角C与θ角的关系,由诱导公式和两角和的正弦公式得sinC,由正弦定理得AC、BC的长度,进而得出要求的量.
解答:(1)sinθ=
,θ是锐角,所以tanθ=
(1分),
tanC=tan[π-(θ+450)]=-tan(θ+450)(2分),
=-
(4分),
=-
=-
(5分).
(2)sinC=sin(θ+450)=
(7分),
由正弦定理
=
=
(9分),
得AC=
×sin450=520(11分),
BC=200
(13分),
新的飞行路程比原路程多AC+BC-AB=520+200
-680=122.8(km)(14分).
| 5 |
| 13 |
| 5 |
| 12 |
tanC=tan[π-(θ+450)]=-tan(θ+450)(2分),
=-
| tanθ+tan450 |
| 1-tanθ•tan450 |
=-
| ||
1-
|
| 17 |
| 7 |
(2)sinC=sin(θ+450)=
17
| ||
| 26 |
由正弦定理
| AB |
| sinC |
| AC |
| sin450 |
| BC |
| sinθ |
得AC=
| AB |
| sinC |
BC=200
| 2 |
新的飞行路程比原路程多AC+BC-AB=520+200
| 2 |
点评:本题考查解三角形的实际应用,做这类是需要仔细观察,要求的量与已知的量有什么样的关系,一一破解;
本题用到的知识点有诱导公式,两角和公式,正弦定理,正弦定理在解三角形时,用于下面两种情况:一是知两边一对角,二是知两角和一边.
本题用到的知识点有诱导公式,两角和公式,正弦定理,正弦定理在解三角形时,用于下面两种情况:一是知两边一对角,二是知两角和一边.

练习册系列答案
相关题目
 如图,一架飞机原计划从空中A处直飞相距680km的空中B处,为避开直飞途中的雷雨云层,飞机在A处沿与原飞行方向成θ角的方向飞行,在中途C处转向与原方向线成45°角的方向直飞到达B处.已
如图,一架飞机原计划从空中A处直飞相距680km的空中B处,为避开直飞途中的雷雨云层,飞机在A处沿与原飞行方向成θ角的方向飞行,在中途C处转向与原方向线成45°角的方向直飞到达B处.已
 ,
,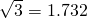 )
) .
. =1.414,
=1.414, =1.732)
=1.732) 

 ,
, )
)

 ,
, )
)