设椭圆C1、抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于表中:
(1)求C1、C2的标准方程;
(2)设直线l与椭圆C1交于不同两点M、N,且
•
=0,请问是否存在这样的直线l过抛物线C2的焦点F?若存在,求出直线l的方程;若不存在,说明理由.
| x | 3 | -2 | 4 |
|
| ||||||||
| y | -2
|
0 | -4 |
|
-
|
(2)设直线l与椭圆C1交于不同两点M、N,且
| OM |
| ON |
设f(x)=
,M=f(1)+f(2)+…+f(2009)则下列结论正确的是( )
| 1 |
| x2 |
| A、M<1 | ||
B、M=
| ||
| C、M<2 | ||
D、M>
|
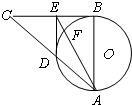 如图:在Rt∠ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:BE•CE=EF•EA.
如图:在Rt∠ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:BE•CE=EF•EA. 12、如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去,则a2009+a2010+a2011等于( )
12、如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去,则a2009+a2010+a2011等于( )