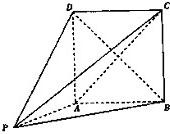
如图，在几何体P-ABCD中，四边形ABCD为矩形，PA⊥平面ABCD，AB=PA=2．（1）当AD=2时，求证：平面PBD⊥平面PAC；
（2）若PC与AD所成角为45°，求几何体P-ABCD的体积．
某研究小组为了研究中学生的身体发育情况，某学校随机抽出20名15至16周岁的男生，将他们的身高和体重制成2×2列联表，根据表联表的数据，可以有 %的把握认为该学校15至16周岁的男生的身高和体重之间有关系．
独立性检验临界值表
独立性检验随机变量K2值的计算公式：K2=
．
| 超重 | 不超重 | 合计 | |
| 偏高 | 4 | 1 | 5 |
| 不偏高 | 3 | 12 | 15 |
| 合计 | 7 | 13 | 20 |
| P（K2≥k0） | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
已知集合M={1，2，3}，N={1，2，3，4}，定义函数f：M→N．若点A（1，f（1））、B（2，f（2））、C（3，f（3）），△ABC的外接圆圆心为D，且
+
=λ
(λ∈R)，则满足条件的函数f（x）有（ ）
| DA |
| DC |
| DB |
| A、6个 | B、10个 |
| C、12个 | D、16个 |
定义方程f（x）=f′（x）的实数根x0叫做函数f（x）的“新驻点”，若函数g（x）=x，h（x）=ln（x+1），φ（x）=x3-1的“新驻点”分别为α，β，γ，则α，β，γ的大小关系为（ ）
| A、α＞β＞γ | B、β＞α＞γ | C、γ＞α＞β | D、β＞γ＞α |
与圆（x-4）2+y2=9相切，且在两坐标轴上截距互为相反数的直线共有（ ）
| A、2条 | B、3条 | C、4条 | D、6条 |
抛物线y2=8x的焦点到双曲线
-
=1的渐近线的距离为（ ）
| x2 |
| 12 |
| y2 |
| 4 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|