在△ABC中，B（-2，0），C（2，0），A（x，y），给出△ABC满足的条件，就能得到动点A的轨迹方程，下表给出了一些条件及方程：
则满足条件①、②、③的轨迹方程分别为 （用代号C1、C2、C3填入）．
则满足条件①、②、③的轨迹方程分别为
| 条 件 | 方 程 | ||||
| ①△ABC的周长为10 | C1：y2=25 | ||||
| ②△ABC的面积为10 | C2：x2+y2=4（y≠0） | ||||
| ③△ABC中，∠A=90° | C3：
|
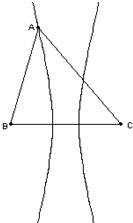如图所示的曲线是以锐角△ABC的顶点B、C为焦点，且经过点A的双曲线，若△ABC的内角的对边分别为a，b，c，且a=4，b=6，| csinA |
| a |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、3-
| ||||
D、3+
|
已知正整数a，b满足4a+b=30，使得
+
取最小值时的实数对（a，b）是（ ）
| 1 |
| a |
| 1 |
| b |
| A、（4，14） |
| B、（5，10） |
| C、（6，6） |
| D、（7，2） |
如图过抛物线y2=2px（p＞0）的焦点F的直线依次交抛物线及准线于点A，B，C，若|BC|=2|BF|，且|AF|=3，则抛物线的方程为（ ）A、y2=
| ||
| B、y2=9x | ||
C、y2=
| ||
| D、y2=3x |
如果
+
=-1表示焦点在y轴上的双曲线，那么它的半焦距c的取值范围是（ ）
| x2 |
| |k|-2 |
| y2 |
| 1-k |
| A、（1，+∞） |
| B、（0，2） |
| C、（2，+∞） |
| D、（1，2） |
某人要作一个三角形，要求它的三条高的长度分别是
、
、
，则此人（ ）
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 6 |
| A、能作出一个钝角三角形 |
| B、能作出一个直角三角形 |
| C、能作出一个锐角三角形 |
| D、不能作出满足要求的三角形 |
已知{an}是等比数列，a2=2，a5=
，则a1a2+a2a3+…+anan+1（n∈N*）的取值范围是（ ）
| 1 |
| 4 |
| A、[12，16] | ||||
B、[8，
| ||||
C、[8，
| ||||
D、[
|