【题目】经观测,某昆虫的产卵数![]() 与温度
与温度![]() 有关,现将收集到的温度
有关,现将收集到的温度![]() 和产卵数
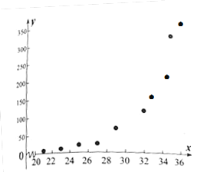
和产卵数![]() 的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
|
|
|
|
|
|
275 | 731.1 | 21.7 | 150 | 2368.36 | 30 |
表中![]() ,
,![]()
(1)根据散点图判断,![]() ,
,![]() 与
与![]() 哪一个适宜作为
哪一个适宜作为![]() 与
与![]() 之间的回归方程模型?(给出判断即可,不必说明理由)
之间的回归方程模型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据.
①试求![]() 关于
关于![]() 回归方程;
回归方程;
②已知用人工培养该昆虫的成本![]() 与温度
与温度![]() 和产卵数
和产卵数![]() 的关系为
的关系为![]() ,当温度
,当温度![]() (
(![]() 取整数)为何值时,培养成本的预报值最小?
取整数)为何值时,培养成本的预报值最小?
附:对于一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为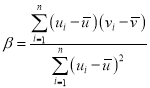 ,
,![]() .
.
【题目】已知函数![]() 的定义域为[-1,5],部分对应值如下表,
的定义域为[-1,5],部分对应值如下表,![]() 的导函数
的导函数![]() 的图象如图所示,下列关于
的图象如图所示,下列关于![]() 的命题正确的是( )
的命题正确的是( )
|
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
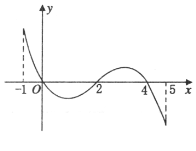
A.函数![]() 的极大值点为0,4;
的极大值点为0,4;
B.函数![]() 在[0,2]上是减函数;
在[0,2]上是减函数;
C.如果当![]() 时,
时,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最大值为4;
的最大值为4;
D.函数![]() 的零点个数可能为0、1、2、3、4个.
的零点个数可能为0、1、2、3、4个.
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
仅使用A | 18人 | 9人 | 3人 |
仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.

