【题目】甲、乙、丙三人去某地务工,其工作受天气影响,雨天不能出工,晴天才能出工.其计酬方式有两种,方式一:雨天没收入,晴天出工每天![]() 元;方式而:雨天每天
元;方式而:雨天每天![]() 元,晴天出工每天
元,晴天出工每天![]() 元;三人要选择其中一种计酬方式,并打算在下个月(
元;三人要选择其中一种计酬方式,并打算在下个月(![]() 天)内的晴天都出工,为此三人作了一些调查,甲以去年此月的下雨天数(
天)内的晴天都出工,为此三人作了一些调查,甲以去年此月的下雨天数(![]() 天)为依据作出选择;乙和丙在分析了当地近
天)为依据作出选择;乙和丙在分析了当地近![]() 年此月的下雨天数(
年此月的下雨天数(![]() )的频数分布表(见下表)后,乙以频率最大的
)的频数分布表(见下表)后,乙以频率最大的![]() 值为依据作出选择,丙以
值为依据作出选择,丙以![]() 的平均值为依据作出选择.
的平均值为依据作出选择.
| 8 | 9 | 10 | 11 | 12 | 13 |
频数 | 3 | 1 | 2 | 0 | 2 | 1 |
(Ⅰ)试判断甲、乙、丙选择的计酬方式,并说明理由;
(Ⅱ)根据统计范围的大小,你觉得三人中谁的依据更有指导意义?
(Ⅲ)以频率作为概率,求未来三年中恰有两年,此月下雨不超过![]() 天的概率.
天的概率.
【题目】为了解中学生对交通安全知识的掌握情况,从农村中学和城镇中学各选取100名同学进行交通安全知识竞赛.下图1和图2分别是对农村中学和城镇中学参加竞赛的学生成绩按![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
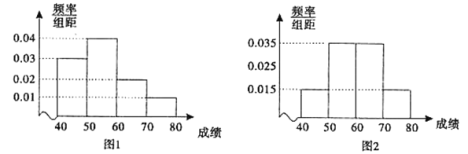
(Ⅰ)分别估算参加这次知识竞赛的农村中学和城镇中学的平均成绩;
(Ⅱ)完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
农村中学 | |||
城镇中学 | |||
合计 |
附:![]()
临界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
【题目】一只药用昆虫的产卵数![]() 与一定范围内的温度
与一定范围内的温度![]() 有关,现收集了该种药用昆虫的
有关,现收集了该种药用昆虫的![]() 组观测数据如下表:
组观测数据如下表:
温度 |
|
|
|
|
|
|
产卵数 |
|
|
|
|
|
|
经计算得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,线性回归模型的残差平方和
,线性回归模型的残差平方和![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 分别为观测数据中的温差和产卵数,
分别为观测数据中的温差和产卵数, ![]() .
.
(1)若用线性回归方程,求![]() 关于
关于![]() 的回归方程
的回归方程![]() (精确到
(精确到![]() );
);
(2)若用非线性回归模型求得![]() 关于
关于![]() 回归方程为
回归方程为![]() ,且相关指数
,且相关指数![]() .
.
(i)试与(1)中的回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
(ii)用拟合效果好的模型预测温度为![]() 时该种药用昆虫的产卵数(结果取整数).
时该种药用昆虫的产卵数(结果取整数).
附:一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为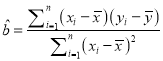 ,
, ![]() ;相关指数
;相关指数