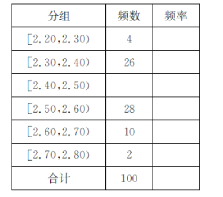
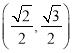【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但蔬菜上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水![]() (单位:千克)清洗蔬菜
(单位:千克)清洗蔬菜![]() 千克后,蔬菜上残留的农药
千克后,蔬菜上残留的农药![]() (单位:微克)的统计表:
(单位:微克)的统计表:
|
|
|
|
|
|
|
|
|
|
|
|
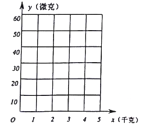
(1)在下面的坐标系中,描出散点图,并判断变量![]() 与
与![]() 是正相关还是负相关;
是正相关还是负相关;
(2)若用解析式![]() 作为蔬菜农药残量
作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程,令
的回归方程,令![]() ,计算平均值
,计算平均值![]() 与
与![]() ,完成以下表格(填在答题卡中),求出
,完成以下表格(填在答题卡中),求出![]() 与
与![]() 的回归方程.(
的回归方程.(![]() 保留两位有效数字);
保留两位有效数字);
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
(3)对于某种残留在蔬菜上的农药,当它的残留量低于![]() 微克时对人体无害,为了放心食用该蔬菜,请评估需要用多少千克的清水清洗一千克蔬菜?(精确到
微克时对人体无害,为了放心食用该蔬菜,请评估需要用多少千克的清水清洗一千克蔬菜?(精确到![]() ,参考数据
,参考数据![]() )(附:对于一组数据
)(附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: 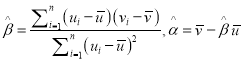 )
)
【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?