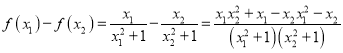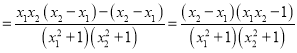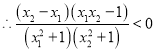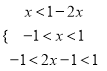0 258808 258816 258822 258826 258832 258834 258838 258844 258846 258852 258858 258862 258864 258868 258874 258876 258882 258886 258888 258892 258894 258898 258900 258902 258903 258904 258906 258907 258908 258910 258912 258916 258918 258922 258924 258928 258934 258936 258942 258946 258948 258952 258958 258964 258966 258972 258976 258978 258984 258988 258994 259002 266669