4.已知函数f(x)=ln(1+x)-ln(1-x).
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求证:当x∈(0,1)时,$f(x)>2({x+\frac{x^3}{3}})$.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求证:当x∈(0,1)时,$f(x)>2({x+\frac{x^3}{3}})$.
3.方程x3-3x+c=0恰有两个实数根,则c=( )
| A. | -2或2 | B. | -9或3 | C. | -1或1 | D. | -3或1 |
2.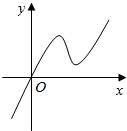 已知函数f(x)的定义域为R,且满足f(4)=1,f′(x)为f(x)的导函数,又知y=f′(x)的图象如图所示,若两个正数a,b满足,f(2a+b)<1,则$\frac{b+2}{a+1}$的取值范围是( )
已知函数f(x)的定义域为R,且满足f(4)=1,f′(x)为f(x)的导函数,又知y=f′(x)的图象如图所示,若两个正数a,b满足,f(2a+b)<1,则$\frac{b+2}{a+1}$的取值范围是( )
 已知函数f(x)的定义域为R,且满足f(4)=1,f′(x)为f(x)的导函数,又知y=f′(x)的图象如图所示,若两个正数a,b满足,f(2a+b)<1,则$\frac{b+2}{a+1}$的取值范围是( )
已知函数f(x)的定义域为R,且满足f(4)=1,f′(x)为f(x)的导函数,又知y=f′(x)的图象如图所示,若两个正数a,b满足,f(2a+b)<1,则$\frac{b+2}{a+1}$的取值范围是( )| A. | $({\frac{2}{3},6})$ | B. | $[{\frac{2}{3},6}]$ | C. | $[\frac{1}{4},\frac{5}{2}]$ | D. | $({\frac{1}{4},\frac{5}{2}})$ |
1.已知下列各组命题,其中p是q的充分必要条件的是( )
| A. | p:m≤-2或m≥6;q:y=x2+mx+m+3有两个不同的零点 | |
| B. | p:$\frac{f(-x)}{f(x)}$=1;q:y=f(x)是偶函数 | |
| C. | p:cos α=cos β;q:tan α=tan β | |
| D. | p:A∩B=A;q:A⊆U,B⊆U,∁UB⊆∁UA |
19.已知数列{an}满足a1=1,an+1=an+2n,则a10=( )
| A. | 1 024 | B. | 1 023 | C. | 2 048 | D. | 2 047 |
18.下列四个数列中,是递增数列的是( )
0 251001 251009 251015 251019 251025 251027 251031 251037 251039 251045 251051 251055 251057 251061 251067 251069 251075 251079 251081 251085 251087 251091 251093 251095 251096 251097 251099 251100 251101 251103 251105 251109 251111 251115 251117 251121 251127 251129 251135 251139 251141 251145 251151 251157 251159 251165 251169 251171 251177 251181 251187 251195 266669
| A. | $\left\{{\frac{n+1}{n}}\right\}$ | B. | $\left\{{\frac{{{{({-1})}^n}}}{n}}\right\}$ | C. | $\left\{{cos\frac{π}{n}}\right\}$ | D. | $\left\{{sin\frac{π}{n}}\right\}$ |