11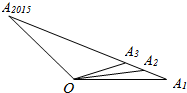．如图.O为直线A1A2015外一点.若A1.A2.A3.A4.A5-A2015中任意相邻两点的距离相等.设${\overrightarrow{OA}} {1}=\overrightarrow{a——青夏教育精英家教网——

如图，O为直线A₁A₂₀₁₅外一点，若A₁，A₂，A₃，A₄，A₅…A₂₀₁₅中任意相邻两点的距离相等，设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$，$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$，用$\overrightarrow{a}，\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$，其结果为（　　）

2014（$\overrightarrow{a}+\overrightarrow{b}$）

2015（$\overrightarrow{a}+\overrightarrow{b}$）

$\frac{2014}{2}$（$\overrightarrow{a}+\overrightarrow{b}$）

$\frac{2015}{2}$（$\overrightarrow{a}+\overrightarrow{b}$）

10．设函数f（x）=e^x（2x-1）+ax-a，其中a＞-1，若关于x不等式f（x）＜0的整数解有且只有一个，则实数a的取值范围为（　　）

（-1，$\frac{3}{2e}$]

（-$\frac{3}{4}$，$\frac{3}{2e}$]

（-$\frac{3}{4}$，-$\frac{3}{2e}$]

（-1，-$\frac{3}{2e}$]

9．若函数f（x）=x²-e^x-ax在R上存在单调递增区间，则实数a的最大值为2ln2-2．

8．若一动直线x=a与函数$f（x）=2{cos^2}（\frac{π}{4}+x）$，g（x）=$\sqrt{3}$cos2x的图象分别交于MN两点，则|MN|的最大值是（　　）

7．现有质地均匀、大小相同、颜色分别为红、黄、蓝的小球各3个，从中随机抽取n个球（1≤n≤9），
（1）当n=3时，记事件A={抽取的三个小球中恰有两个小球颜色相同}．求P（A）；
（2）当n=2时，若用ξ表示抽到的红球的个数．
①求ξ的概率分布；
②令η=-λ²ξ+λ+1，E（η）＞1．求实数λ的取值范围．

6．角α始边与x轴非负半轴重合，终边经过点P（-2，1），则tanα=-$\frac{1}{2}$．

5．定义在R上的偶函数f（x），且f（x）在[0，+∞）上单调递减，则不等式f（lgx）＜f（1）的解集是（$\frac{1}{10}$，10）．

4．已知下列四个命题：
①若函数y=f（x）在定义域上为减函数，则函数y=-f（x）在定义域上为增函数；
②若函数y=f（x）在定义域上为增函数，则函数g（x）=$\frac{1}{f（x）}$在其定义域内为减函数；
③若函数y=1+log_a（x-1）图象过定点P（m，n），则log_mn=0；
④若函数y=f（x）和y=g（x）在区间[-a，a]上都是奇函数，则函数y=f（x）•g（x）在区间[-a，a]上是偶函数，其中正确命题的序号是①④．

3．设幂函数f（x）=（a-1）x^k图象过点$（\sqrt{2}，2）$，则实数a+k的值为4．

2．已知函数f（x）=$\left\{\begin{array}{l}1-2|x-\frac{1}{2}|，0≤x≤1\\{log_{2014}}x，\;\;\;\;\;x＞1\end{array}$，若直线y=m与函数y=f（x）三个不同交点的横坐标依次为x₁，x₂，x₃且x₁＜x₂＜x₃，则x₃的取值范围是（　　）

0 250787 250795 250801 250805 250811 250813 250817 250823 250825 250831 250837 250841 250843 250847 250853 250855 250861 250865 250867 250871 250873 250877 250879 250881 250882 250883 250885 250886 250887 250889 250891 250895 250897 250901 250903 250907 250913 250915 250921 250925 250927 250931 250937 250943 250945 250951 250955 250957 250963 250967 250973 250981 266669