1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),F1,F2分别是它的左、右焦点,A是它的右顶点,过点F1作一条斜率为k的直线交双曲线于异于顶点的两点M、N,若∠MAN=90°,则该双曲线的离心率为( )
0 249788 249796 249802 249806 249812 249814 249818 249824 249826 249832 249838 249842 249844 249848 249854 249856 249862 249866 249868 249872 249874 249878 249880 249882 249883 249884 249886 249887 249888 249890 249892 249896 249898 249902 249904 249908 249914 249916 249922 249926 249928 249932 249938 249944 249946 249952 249956 249958 249964 249968 249974 249982 266669
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
 如图,在四棱锥P-ABCD中,已知侧面PAD为等腰三角形,底面ABCD为直角梯形,AB∥CD,∠ABC=∠APD=90°,侧面PAD⊥底面ABCD,且AB=4,AP=PD=BC=CD=2.
如图,在四棱锥P-ABCD中,已知侧面PAD为等腰三角形,底面ABCD为直角梯形,AB∥CD,∠ABC=∠APD=90°,侧面PAD⊥底面ABCD,且AB=4,AP=PD=BC=CD=2.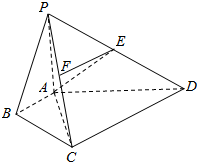 在四棱锥P-ABCD中,∠ABC=$\frac{π}{2}$,∠BAC=∠CAD=$\frac{π}{3}$,PA⊥平面ABCD,E为PD的中点,PA=2AB=2,CD=2$\sqrt{3}$.
在四棱锥P-ABCD中,∠ABC=$\frac{π}{2}$,∠BAC=∠CAD=$\frac{π}{3}$,PA⊥平面ABCD,E为PD的中点,PA=2AB=2,CD=2$\sqrt{3}$.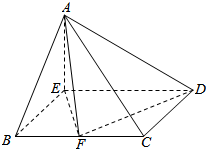 如图所示,在四棱锥A-BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.
如图所示,在四棱锥A-BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.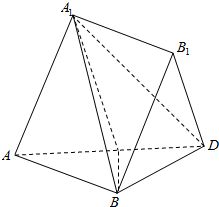 如图,多面体A1B1-ABC中,△ABC与△AA1C都是边长为2的正三角形,四边形ABB1A1是平行四边形,且平面A1AC⊥平面ABC.
如图,多面体A1B1-ABC中,△ABC与△AA1C都是边长为2的正三角形,四边形ABB1A1是平行四边形,且平面A1AC⊥平面ABC.