题目内容
12.数列{an}满足Sn=2n-an(n∈N*)(1)计算a1,a2,a3,a4,由此猜想通项公式an,并用数学归纳法证明此猜想;
(2)若数列{bn}满足bn=2n-1an,求证:$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$<$\frac{5}{3}$.
分析 (1)令n=1,2,3,4,可得前4项,再由数学归纳法即可得证;
(2)求得bn,再由放缩法证明,即为$\frac{1}{{2}^{k}-1}$<$\frac{2}{{2}^{k}-1}$-$\frac{2}{{2}^{k+1}-1}$,运用裂项相消法,从第二项放缩即可得证.
解答 解:(1)由Sn=2n-an(n∈N*),
可得a1=S1=2-a1,可得a1=1,
a2=S2-S1=4-a2-1,可得a2=$\frac{3}{2}$,
a3=S3-S2=6-a3-$\frac{5}{2}$,可得a3=$\frac{7}{4}$,
a4=S4-S3=8-a4-$\frac{17}{4}$,可得a4=$\frac{15}{8}$,
猜想得到an=$\frac{{2}^{n}-1}{{2}^{n-1}}$,
由数学归纳法可得.
当n=1时,a1=1,$\frac{2-1}{{2}^{0}}$=1,成立;
设n=k时,ak=$\frac{{2}^{k}-1}{{2}^{k-1}}$成立,
当n=k+1时,ak+1=Sk+1-Sk=2(k+1)-ak+1-2k+ak,
可得ak+1=$\frac{1}{2}$(2+ak)=$\frac{1}{2}$(2+$\frac{{2}^{k}-1}{{2}^{k-1}}$)=$\frac{{2}^{k+1}-1}{{2}^{k}}$,
即有n=k+1也成立.
综上可得an=$\frac{{2}^{n}-1}{{2}^{n-1}}$,对n为一切非零自然数成立.
(2)证明:bn=2n-1an=2n-1,
即证1+$\frac{1}{3}$+$\frac{1}{7}$++…+$\frac{1}{{2}^{n}-1}$<$\frac{5}{3}$.
由$\frac{1}{{2}^{k}-1}$<$\frac{2}{{2}^{k}-1}$-$\frac{2}{{2}^{k+1}-1}$,
等价于:2k+1-2<2k+1-1;
所以:①当n=1时,原不等式成立,
②当n≥2时,1+$\frac{1}{3}$+$\frac{1}{7}$+…+$\frac{1}{{2}^{n}-1}$≤1+($\frac{2}{3}$-$\frac{2}{7}$)+($\frac{2}{7}$-$\frac{2}{15}$)+…+($\frac{2}{{2}^{n}-1}$-$\frac{2}{{2}^{n+1}-1}$)
=1+$\frac{2}{3}$-$\frac{2}{{2}^{n+1}-1}$=$\frac{5}{3}$-$\frac{2}{{2}^{n+1}-1}$<$\frac{5}{3}$.
即有不等式成立.
点评 本题考查数列的通项的求法,考查数学归纳法的运用和放缩法的运用:证明不等式,属于中档题.

| A. | $\frac{16}{9}$ | B. | $\frac{4}{3}$ | C. | $\frac{9}{16}$ | D. | $\frac{3}{4}$ |
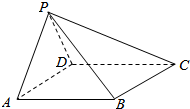 如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°.
如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°.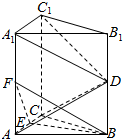 在直三棱柱ABC-A1B1C1中,D、E、F分别是BB1、AA1、AC的中点,AC=BC=$\frac{1}{2}$AA1,AB=$\sqrt{2}$AC
在直三棱柱ABC-A1B1C1中,D、E、F分别是BB1、AA1、AC的中点,AC=BC=$\frac{1}{2}$AA1,AB=$\sqrt{2}$AC