18.设函数y=f(x)定义域为{x|x∈R且x≠1},已知f(x+1)为奇函数,当x<1时,f(x)=2x2-x+1,则x>1时,f(x)的递减区间为( )
| A. | [$\frac{5}{4}$,+∞) | B. | (1,$\frac{5}{4}$] | C. | [$\frac{7}{4}$,+∞) | D. | (1,$\frac{7}{4}$] |
17.已知等比数列{an}的公比q=$\frac{1}{2}$,且a2+a4+…+a100=30,则a1+a2+…+a100=( )
| A. | 100 | B. | 90 | C. | 120 | D. | 30 |
14.某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如图).记成绩不低于90分者为“成绩优秀”.
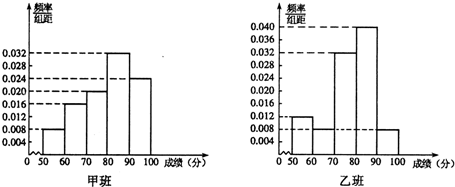
(1)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为ξ,求ξ的分布列和数学期望;
(2)根据频率分布直方图填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
0 249695 249703 249709 249713 249719 249721 249725 249731 249733 249739 249745 249749 249751 249755 249761 249763 249769 249773 249775 249779 249781 249785 249787 249789 249790 249791 249793 249794 249795 249797 249799 249803 249805 249809 249811 249815 249821 249823 249829 249833 249835 249839 249845 249851 249853 249859 249863 249865 249871 249875 249881 249889 266669

(1)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为ξ,求ξ的分布列和数学期望;
(2)根据频率分布直方图填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关.
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
 PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.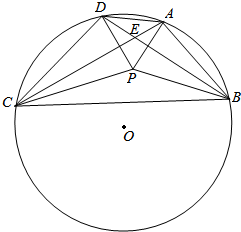 凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.
凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.